Mathematik
mit einer wechselnden Auswahl von Unterrichtsmaterialen zur
Mathematik sowie Verweisen ("Links") auf fremde
Internetseiten.
Im Moment finden Sie hier
- Vorbemerkung zur Darstellung,
pdf-Anzeige und evtl. Download-Problemen dieser
Webseite
- Veranstaltungen, Mathe-Wettbewerbe und -Adventskalender,
Corona-Mathematik
- Klausuren, Klassenarbeiten, Arbeitsblätter,
Unterrichtsentwürfe, Lehrpläne und
Abituranforderungen
- Mathematische Fähigkeiten, Anwendungsbezug &
Realitätsnähe des Mathe-Unterrichts
- Stochastik in Unterricht und Alltag
- Analysis in Unterricht und Alltag
- Zahlentheorie
- Rezensionen von Mathe-Software und -Büchern
- sowie viele Verweise auf fremde
Web-Seiten zur Mathematik (2024 aktualisiert)
Internet-Darstellung, Probleme &
Download
Diese Seiten sind nicht für Smartphones, sondern für
das Betrachten an größeren Bildschirmen (PCs, Laptops
bzw. Notebooks, Tablets..) konzipiert.
Während Ihnen der Druck meiner Seiten problemlos gelingen
sollte (weil ich extra keine Frames oder dynamische Inhalte
verwende), müssen Sie beim Speichern auf Ihre Festplatte
aufpassen, dass Ihr Browser auch die Bilder speichert. Als Bilder
gelten auch Formeln! Wählen Sie dazu nach Strg+S bzw.
["Seite" >] "Speichern unter.." als Dateityp "Webseite,
komplett (*.htm, *.html)" oder "Webseite, vollständig (*htm,
*html)".
Da es umgekehrt mühsam ist, alle Formeln, Sonderzeichen,
Abbildungen u.ä. einzeln in Bilder zu konvertieren und damit
die Arbeitblätter ins Netz zu stellen -- zumal HTML nicht
alle Formatierungen kennt, das Ergebnis also trotzdem oft
unbefriedigend bleibt --, habe ich entweder (z.B. bei den
Lösungen meiner Klassenarbeiten) direkt seitengroße
Bilder integriert oder habe viele Beiträge im pdf-Format
bereitgestellt. Inzwischen ist mit fast allen Internet-Browser
die pdf-Anzeige möglich. Wenn die Anzeige nicht
überzeugt, kann nach Installation eines zusätzlichen
pdf-Readers der Browser meist so eingestellt werden, dass er das
fremde (bessere) Anzeigeprogramm verwendet!
Kostenlose pdf-Reader sind z.B. der bekannte Adobe-Reader,
aber auch die meist kompakteren und z.T. besseren FoxIt- ,
Safari-, Nuance-Pdf- oder der Perfect-Pdf-Reader bzw. der
Pdf-XChange-Viewer, um nur einige zu nennen).
zum Seitenanfang / zum Seitenende
Veranstaltungen, Mathe-Wettbewerbe und
-Adventskalender, Corona-Mathematik
14.3.2025
Sechster Internationaler Tag der Mathematik
Hervorgegangen aus dem früheren Pi-Tag (pi day; das Datum
14. März bzw. 14.3. zeigt in amerikanischer Schreibweise
3/14 die ersten drei Ziffern der Kreiszahl Pi = 3.14...) *), wird
auf Beschluss der Unesco seit 2020 immer am 14.
März der Internationale Tag der Mathematik gefeiert; 2020
also zum ersten Mal unter dem neuen Titel. Zwar erwähnt
kleiner-kalender.de selbst in der Ankündigung
für 2025 nur die Kreiszahl, aber die offizielle Seite
idm314.org
(englisch) oder - in Deutsch: - kuriose-feiertage.de und natürlich
Wikipedia liefern viele Informationen zum
Festtag, seiner Entstehung und den Zielen. In den verschiedenen
Jahren stehen immer wieder andere Themen im Vordergrund:
- 2020 Mathe ist überall
- 2021 Mathe verbessert die Welt
- 2022 Mathematik verbindet / Bilder mit
Mathe
- 2023 Mathematik für jeden/alle (inkl.
Mathe-Comics)
- 2024 Spiele mit Mathematik (aber auch Spielen
mit Mathematik, d.h. mit mathematischen Ideen, Verfahren,
Strukturen..)
- 2025 Mathematik, Kunst und
Kreativität
Mathe-Lehrerinnen und -lehrer sind aufgerufen, an diesem Tag
die Bedeutung des Fachs durch ein Event oder eine geeignete
Aktion in ihrer Schule ins Bewusstsein möglichst vieler
Schülerinnen und Schüler (am besten auch der
Nicht-Fachkolleg[inn]en) zu heben.
An und um diesen Tag herum bieten Mathematische Institute
einiger Hochschulen Sonderveranstaltungen an oder nehmen den Tag
zum Anlass, Schülerinnen und Schüler über das
Mathematik-Studium zu informieren. Auch manche Schulen bewerben
ihre Projekte im Internet - also bitte nach Angeboten in Ihrer
Nähe suchen; oft muss man sich für eine Teilnahme
frühzeitig anmelden!
Während z.B. die Uni Münster auch dieses Jahr wieder
mehrere interessante Angebote macht, bin ich 2025 von der
Heinrich-Heine-Universität (HHU) in Düsseldorf etwas
enttäuscht: Nach einer Reihe vielversprechender Aktionen in
der Uni und auch für eine breite Öffentlichkeit im Haus
der Universität in der Innenstadt, die für den ersten
Tag der Mathematik 2020 aufwändig vorbereitet worden waren
(und dann kurzfristig wegen Corona abgesagt werden mussten) und
weiteren, immer noch im Netz zu findenden Präsentationen von
Doktoranden 2022 scheint der Elan jetzt etwas erlahmt - zumindest
habe ich Anfang Februar 2025 hier keine Ankündigung für
besondere Vorträge oder Veranstaltungen in Düsseldorf
im Internet gefunden. Social-Media-Kanäle habe ich
allerdings nicht geprüft.
 *)
Den Namen "pi" erhielt die Kreiszahl 1706 vom walisischen
Mathematiker William Jones (1675 - 1749). Sie ist bekanntlich der
Quotient aus Umfang und Durchmesser eines/jedes Kreises. Und weil
Umfang griechisch Peripherie und Durchmesser auf griechisch
Perimeter heißt, beide griechischen Wörter also mit p
anfangen, wählte William Jones das griechische p,
nämlich
*)
Den Namen "pi" erhielt die Kreiszahl 1706 vom walisischen
Mathematiker William Jones (1675 - 1749). Sie ist bekanntlich der
Quotient aus Umfang und Durchmesser eines/jedes Kreises. Und weil
Umfang griechisch Peripherie und Durchmesser auf griechisch
Perimeter heißt, beide griechischen Wörter also mit p
anfangen, wählte William Jones das griechische p,
nämlich 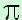 , als Symbol.
Durchgesetzt hat sich die Bezeichnung, nachdem sie 1737 auch von
Leonard Euler aufgegriffen und verwendet wurde.
, als Symbol.
Durchgesetzt hat sich die Bezeichnung, nachdem sie 1737 auch von
Leonard Euler aufgegriffen und verwendet wurde.
zum Seitenanfang / zum Seitenende
Mathematik-Wettbewerbe 2025
Soweit die Anmeldefristen für die
2025er-Wettbewerbe beim verspäteten Lesen dieser Seite schon
abgelaufen sind, bleibt nur das Warten auf das nächste
Jahr!
Neben den Adventskalendern (s.u.) gibt es viele weitere
jährlich durchgeführte Mathematik-Wettbewerbe. Hier
einige wichtige Möglichkeiten mit aktuellen Terminen:
- Am Känguru-Wettbewerb jeweils im
Frühjahr nehmen ganze Schulen teil bzw. werden
Schülerinnen und Schüler von ihren Lehrerinnen oder
Lehrern angesprochen. Näheres findet sich auf https://www.mathe-kaenguru.de; Lehrkräfte
konnten sich bzw. ihre Schulen bis zum
31.1.2025 für den Termin am 20.
März 2025 anmelden. Pro Teilnehmer wird ein
Startgeld von 2,50 € erhoben, das an vielen Schulen die
Fördervereine tragen.
- Der 18. Pangea-Mathematik-Wettbewerb unter
der Schirmherrschaft des deutschen Bundesministeriums für
Bildung und Forschung richtet sich an alle(!) Schülerinnen
und Schüler der Klassen 3 bis 10 und zielt nicht nur auf
besonders Begabte oder Leistungsstarke ab. Erklärtes Ziel
ist es, auch Mathe-Muffeln wieder zu Spaß am Fach zu
verhelfen und eventuelle Angst vor Mathematik zu nehmen. Die
Anmeldung zum Wettbewerb 2024 muss bis zum 17. Februar
2025 vorgenommen werden und sollte möglichst
durch die Schule erfolgen. Die Vorrunde findet ab dem 25.2.2025
statt; die Zwischenrunde ist für den 2. und 3. April 2025
geplant; Mitte Mai 2025 folgt die Endrunde. Alle Details,
Beispielaufgaben und den Link zum Anmeldeportal gibt's auf
https://www.pangea-wettbewerb.de. Es sind Urkunden,
Präsente und für die Finalisten wertvolle Preise
ausgelobt. Also den Mathe-Lehrer bzw. die Mathe-Lehrerin fragen
und auf den Wettbewerb aufmerksam machen und anmelden lassen
(oder wenn sie selbst vom Fach sind: hin!). Verpasst? Dann
rechtzeitig im Januar 2026 für den nächsten, 19.
Wettbewerb anmelden!
- Am Bundeswettbewerb Mathematik (https://www.mathe-wettbewerbe.de/bundeswettbewerb-mathematik)
kann jede Schülerin oder jeder Schüler teilnehmen,
die/der in Deutschland eine Schule besucht, die zum Abitur
(Hochschulreife) führt. Vom Niveau wird eher die
Sekundarstufe II angesprochen. Die Aufgaben der 1. Runde 2025
sind seit Dezember 2024 online. Herunterladen, lösen und
bis zum 3. März 2025 einschicken -- eine
vorherige Anmeldung ist nicht nötig. Die Korrektur erfolgt
bis Juni 2025; im August 2025 wird dann die zweite Runde
gestartet (Abgabeschluss 1.9.25). Die dritte und letzte Runde
folgt vermutlich Anfang 2026!. Das Aufgabenarchiv zeigt Beispiele früherer
Aufgaben sowohl vom Bundeswettbewerb (BWM) wie von den
nachfolgend erwähnten Mathe-Olympiaden.
- Für die Internationale
Mathematik-Olympiade IMO (https://www.mathematik-olympiaden.de) gibt es Schul-,
Regional- und Landesrunden, bevor man in die Bundesauswahl
(DeMO) kommt und dort nochmal drei Runden bis zum
internationalen Sieg überstehen muss. Im Moment läuft
die 64. Mathe-Olympiade 2024/2025, die zum Schuljahresbeginn
2024 gestartet ist. Die 65. Olympiade beginnt für die
Klassen 5 bis 12 (bzw. 13) im August/September 2025 mit den
Schulrunden; also vor oder spätestens direkt nach
den Sommerferien 2025 rechtzeitig die/den
Mathe-Lehrer(in) ansprechen und die Teilnahme planen, die
hoffentlich mindestens bis zur Bundesrunde im Mai/Juni 2026
führt. Für Grundschüler der Klassen 3 und 4
gelten eventuell abweichende Termine, die von jeder Schule
selbst festlegt werden - frühestens begann/beginnt der
Wettbewerb ab 1. August, spätestens im Dezember. Die
Aufgaben und ihr Schwierigkeitsgrad sind den Klassen- bzw.
Jahrgangsstufen der Teilnehmerinnen und Teilnehmer
angepasst.
- Als Ergänzung für die Vorbereitung zum
Mathematik-Bundeswettbewerb und zu den Mathematik-Olympiaden
gab es 2024 außerdem "Jugend trainiert
Mathematik". Um hierfür eingeladen zu werden und
teilnehmen zu können, musste man bereits
einigermaßen erfolgreich an einem Mathe-Wettbewerb
teilgenommen haben. Mit dem angebotenen Zusatztraining soll die
nächste Wettbewerbsteilnahme dann noch besser gelingen. Im
Februar 2025 waren auf der Webseite allerdings nur die alten
Termine März 2024 und April 2024 zu sehen; insofern ist
ungewiss, ob das Programm auch 2025 erneut aufgelegt wird: Mehr
Infos auf https://www.mathe-wettbewerbe.de/juma.
- Für die mathematischen Adventskalender gibt's
nachfolgend einen eigenen Abschnitt!
zum Seitenanfang / zum Seitenende
Mathematik-Adventskalender
 Am 1. Dezember 2025 ging es wieder
los: Nach einmaliger Anmeldung konnte man die eigenen
Lösungen täglich per eMail einsenden und damit auf
einen der vielen Gewinne hoffen, die auf die Teilnehmerinnen und
Teilnehmer warten. Aber auch ohne Registrierung kann man - auch
jetzt, nachträglich noch - bei den meisten Angeboten
Türchen öffnen und die Fragen sehen und beantworten.
Denn auch ohne Gewinnchance macht das Rätseln Spaß.
Wer trotzdem auch materielle Preise gewinnen will, sollte sich im
November 2026 für den kommenden Advent anmelden. Und um die
Gewinnchancen zu erhöhen, übt man jetzt am besten schon
an den alten Aufgaben!
Am 1. Dezember 2025 ging es wieder
los: Nach einmaliger Anmeldung konnte man die eigenen
Lösungen täglich per eMail einsenden und damit auf
einen der vielen Gewinne hoffen, die auf die Teilnehmerinnen und
Teilnehmer warten. Aber auch ohne Registrierung kann man - auch
jetzt, nachträglich noch - bei den meisten Angeboten
Türchen öffnen und die Fragen sehen und beantworten.
Denn auch ohne Gewinnchance macht das Rätseln Spaß.
Wer trotzdem auch materielle Preise gewinnen will, sollte sich im
November 2026 für den kommenden Advent anmelden. Und um die
Gewinnchancen zu erhöhen, übt man jetzt am besten schon
an den alten Aufgaben!
Das Deutsche Forschungszentrum MatheOn stellt zusammen mit der
Deutschen Mathematiker-Vereinigung drei Versionen von
mathematischen Adventskalendern mit unterschiedlich schweren
Aufgaben ins Netz:
- unter "Klassen 4-9" zwei Kalender für
Schülerinnen und Schüler der Sekundarstufe I.
Drückt man nämlich zunächst auf die
Schaltfläche 4-9, so kann man schließlich zwischen
zwei Niveaus wählen: entweder Aufgaben für die
Klassen 4 bis 6 und Aufgaben für die Klassen 7 bis 9.
- unter "Klassen 10+" die anspruchsvollste Ausgabe als
digitaler Adventskalender "Math+" ab Klasse 10 bzw. für
die SII (Sekundarstufe II, auch Ober- oder Kollegsstufe)
Selbst die schwierigste Version, der digitale
MatheOn-Adventskalender "Math+" ab Klasse 10, erfordert aber
meist mehr gesunden Menschenverstand und Nachdenken über
praktische Zusammenhänge als unbedingt komplizierte
Rechentechniken, sodass auch Grundkurs-Schülerinnen und
-Schüler gute Chancen haben. Im Advent ließen sich die
aktuellen Türchen immer erst ab 16 Uhr öffnen, damit
Schülerinnen und Schüler mit spätem Schulschluss
nicht zusätzlich benachteiligt wurden. Wer will, kann
jederzeit auch einen Blick auf die interessanten Aufgaben
früherer Jahre werfen: denn bei MATH+ kann man z.B. unter
"Kalender" > "Aufgabenarchiv" Aufgaben und Lösungen
früherer Jahre in absteigender Anordnung jeweils in einer
pdf-Datei zusammen gepackt finden ("Aufgaben und Lösungen
2023" bis "Aufgaben und Lösungen 2004"). Der Kalender vom
Dezember 2025 war Januar 2026 noch funktionsfähig
(Türen öffnen ohne Anmeldung), kommt aber sicher bald
mit Lösungen ins Archiv. Also hin zu den Angeboten für
die unterschiedlichen Altersstufen! Die findet man auf der
gemeinsamen Startseite:
www.mathekalender.de
Bei den beiden niedrigeren Anforderungsstufen kann man z.Z.
nicht nur die Aufgaben vom Dezember 2025, sondern auch deren
Lösungen abrufen. Und: Diese Kalender für die Klassen 4
bis 6 bzw. für die Klassen 7 bis 9 sind zusätzlich auch
über die Webseite MiA = Mathe-im-Advent.de zu erreichen; aufgeweckte
Zweitklässler können sich als "Frühstarter" schon
an den Aufgaben für die Klassen 4-6 versuchen. Umgekehrt
spricht nichts dagegen, dass auch Zehntklässler noch die
Aufgaben der Klassen 7-9 mit Freude und Erfolg bearbeiten (selbst
wenn sie dort deshalb "Spätstarter" genannt werden oder als
"Spaßspieler" teilnehmen).
Im Übrigen lohnt auch sonst im Jahr gelegentlich der
Blick in die Mathekalender - nicht nur um Aufgaben früherer
Jahre anzusehen und zu lösen, sondern auch, weil
gelegentlich zwischendurch neue Aufgaben online gestellt werden:
etwa zu Ostern oder für ein
MiA-Halloween-Rätsel.
Für Grundschüler gab es außerdem von der
Humboldt-Universität Berlin bzw. dem Verein, der den
Känguru-Mathewettbewerb durchführt, zwei weitere
Mathe-Adventskalender, nämlich die Mini-Variante für die 1./2. und die
Maxi-Ausgabe für die 3./4.
Klassenstufe. "Nur so" konnten sich auch Ältere an den
Aufgaben versuchen, denn ein Account kann und braucht dazu nicht
eingerichtet werden. Allerdings gibt es außer Spaß
auch nichts zu gewinnen. Die Aufgabe des Tages wurde sofort beim
Anklicken des vorstehenden Mini- oder Maxi-Links angezeigt
(sodass das Suchen des richtigen Tages in einem bunten Bild mit
24 zufällig angeordneten Türchen leider entfällt).
Da der 24.12.2025 inzwischen vorbei ist, gibt es keine
Tagesaufgabe mehr. Allerdings sind z.Z. am rechten Rand unter
"Hier gibt es alles Nötige zum Drucken" die bisherigen
Tagesaufgaben (also alle vom Dezember 2025) in einer pdf-Datei
abrufbar und am Ende dieser Datei werden sogar die richtigen
Lösungen genannt. Die Kalender der letzten Jahre sind
hingegen in der Tabelle unten auf der Mini- oder Maxi-Seite
verlinkt. Alle früheren Aufgaben (alle
Känguru-Aufgaben, nicht nur die Adventrätsel, z.T.
zurück bis 1998) gibt's auch: Oben auf der Mini- oder
Maxi-Seite ist eine Leiste mit den Reitern 'Home', 'Wettbewerbe',
'Aufgaben', 'Chronik' und 'International'. Klickt man auf den
Reiter 'Aufgaben', kommt man auch zu den älteren Aufgaben
(und Lösungen). Der Mini- und der Maxi- Kalender können
auch erreichet werden über
www.mathe-kaenguru.de/advent
Auf meiner Physik-Seite wird
außerdem (bei den Wettbewerben) auf einen physikalischen
Adventskalender hingewiesen: PIA - Physik im
Advent. Hier konnten Videos von Vorgängen,
Phänomenen oder Experimenten angesehen werden. Dazu wurde
dann eine Frage gestellt, die beantwortet werden muss. 2025
konnte man sich vorab anmelden und Material besorgen oder
vorbereiten, um damit selbst Experimente nach Anleitung
durchzuführen und auszuwerten. Inzwischen ist der Wettbewerb
vorbei. Wer seine Ergebnisse sehen will, muss sich nochmal
anmelden. Wer aber jetzt "nur so" die Aufgaben sehen und
lösen will, klickt oben in der Kopfleiste der Seite auf
'KALENDER' und kann dann auch im Januar 2025 alle Türchen
öffnen. Schade, dass oben sofort das Lösungsvideo
angeboten wird - noch nicht ansehen, sondern etwas runter
scrollen: Darunter findet sich nämlich unter "Experiment"
das Aufgabenvideo und darunter werden nochmal schriftlich die
auch im Video gestellten Fragen wiederholt.
Interessant für alle, die sich gerne mit Geheimschriften
und der Ver- bzw. Entschlüsselung beschäftigten,
wäre der Kalender Krypto im
Advent, herausgegeben von der Karlsruher
IT-Sicherheitsinitiative in Zusammenarbeit mit der dortigen
Pädagogischen Hochschule. 2022 und 2024 war der Wettbewerb
ausgefallen. 2025 sollte wenigstens alle zwei Tage eine Aufgabe
gestellt werden - für angemeldete Personen. Ob das wirklich
geschehen ist, bleibt unklar: Im Januar 2026 sind die Aufgaben
nicht öffentlich einsehbar und auf der Webseite gibt es
immer noch die Ankündigung des angeblich noch kommenden
Wettbewerbs sowie einen Link zu den Rätselbeispielen des
2023 in zwei Versionen durchgeführten Wettbewerbs: für
'Einsteiger' (Klassen 3 bis 6) und für 'Fortgeschrittene'
(Klassen 7 bis 9). Allerdings funktionierten die Links bei mir im
Januar 2026 nicht mehr: Man erhält den Hinweis, dass der
Wettbewerb 2024 ausfällt! Die Erklärvideos (von 2022)
waren über den Verweis (Link) aber auch im Januar 2026 noch
problemlos bei Youtube abrufbar.
Interesse an der Kryptologie? Zwar ohne Filmchen, aber oft mit
herunterlad- und ausführbaren Java-Programmen (Anwendungen
bzw. Applications) findet man ausführliche Informationen und
Erklärungen auf dem Niveau eines Informatik-Leistungskurses
der Oberstufe auf meinen
Informatik-Seiten i) und k) zur Kryptologie, auf denen
klassische
(symmetrische) bzw. moderne (asymmetrische)
Krypto-Verfahren behandelt werden.
Und zum Advent passt natürlich auch das weiter unten auf
dieser Seite besprochene Haus vom
Nikolaus.
zum Seitenanfang / zum Seitenende
Mathematik zur
Corona-Pandemie
Durch die Corona-Pandemie war auch die Mathematik gefordert,
um verschiedenste Behauptungen seriös zu prüfen und die
Diskussion zu versachlichen. Zu Beginn - im Februar und März
2020 - ging es zunächst darum, ein Gespür für das
exponentielle Wachstum zu vermitteln, um die Dringlichkeit z.B.
der AHA-Regeln zu verstehen. Wachstumsmodelle, Auswirkung der
Senkung der Infektionsrate auf die voraussichtliche Dauer der
Pandemie sowie die Erklärung und Berechnung der
Kenngrößen Verdoppelungszeit, 7-Tage-Inzidenz,
Reproduktionsrate R bzw. (7-Tage-) R-Wert wurden nach und nach
hier veröffentlicht ebenso wie Anregungen, die durch
ungeschützte Großereignisse oder Quer-'denker'-Demos
verursachten Todesfälle zu berechnen. Die Abfolge gibt
dadurch auch implizit Hinweise auf die Chronologie des
Covid-Geschehens.
Mathematisch wurden Wachstumsmodelle (insbesondere
exponentielles und logistisches Wachstum, zum Vergleich aber auch
lineares und beschränktes Wachstum) sowie die
Grundrechenarten bzw. arithmetische Mittel benötigt.
Rechnungen und Formeln im Text, drei Tabellenkalkulationsmappen
(auch zum Herunterladen und Ausprobieren/Ändern) sowie die
zusätzliche Modellierung der Wachstumsfälle mit der
Simulationssoftware DynaSys (auf meiner Informatik-Seite)
ergänz(t)en meine Berichte.
Im April 2023 habe ich dann die verschiedenen Artikel zusammen
mit einer abschließenden Würdigung ausgelagert auf
diese
Extraseite: Mathematik zur
Corona-Pandemie
zum Seitenanfang / zum Seitenende
Klausuren, Klassenarbeiten,
Arbeitsblätter, Unterrichtsentwürfe, Lehrpläne und
Abituranforderungen
Materialien &
Klausuren aus der SII
Auf einer Sonderseite gibt's eine einige meiner Klausuren aus
dem Unterricht in der Oberstufe (EF bis Q2). Natürlich
gibt's zu den Aufgaben auch Lösungen, die man sich aber erst
nach eigenem, intensiven Bemühen um die richtigen Resultate
ansehen sollte.
Extra-Seite: Mathe-Klausuren SII
(bis Sommer 2017)
zum Seitenanfang / zum Seitenende
Zentralabitur
Wegen des leider auch in Nordrhein-Westfalen längst
eingeführten Zentralabiturs werden im Mathematik-Unterricht
immer einige kleinere Themenverschiebungen und/oder
veränderte Gewichtungen vorgenommen, um Schülerinnen
und Schülern optimal auf die jeweils für den
Abiturjahrgang angekündigten Prüfungsaufgaben bzw. die
jeweils als besonders wichtig erklärten Themengebiete
vorzubereiten.
Eine Übersicht über Themen sowie die Aufgaben der
letzten Jahre für das Zentralabitur im Gymnasium finden sich
für verschiedene Fächer, u.a. für Mathematik,
auf
https://www.standardsicherung.schulministerium.nrw.de/cms/zentralabitur-gost/faecher/
Andere, über die zentralen Vorgaben hinaus gehende
lehrplanmäßige Stoffe können und sollen
natürlich weiterhin behandelt und in normalen Klausuren und
mündlichen Abiturprüfungen abgefragt werden.
Im Bildungsgang 1 "Abitur mit
Schwerpunkt Mathematik und Informatik" (=Bildungsgang nach Anlage
D21 der APO-BK), der zum Berufskolleg bzw. Beruflichen Gymnasium
gehört, begann das Zentralabitur im Jahr 2008 mit Informatik
und erst 2009 mit Mathematik. Leider wird der Bildungsgang am
Lessing-BK in Düsseldorf nicht mehr angeboten; das letzte
Abitur fand hier 2023 statt. Für den
Mathematik-Leistungskurs dieses Bildungsgangs an anderen Schulen
des Landes NRW findet man auf der folgenden Seite die jeweils
gültigen aktuellen Vorgaben und Hinweise:
https://www.standardsicherung.schulministerium.nrw.de/cms/zentralabitur-berufliches-gymnasium/bildungsgaenge/bildungsgang.php?id=21
Die zugehörigen Richtlinien
('Bildungspläne') stehen auf
https://www.berufsbildung.nrw.de/cms/bildungsgaenge-bildungsplaene/berufliches-gymnasium-anlage-d/bildungsplaene/kff-informatik.html
zum Seitenanfang / zum Seitenende
Lehrplan für
die S I
Die Kernlehrpläne für die Klassen 5 bis 10 der
Gymnasien in Nordrhein-Westfalen berücksichtigen wieder die
Schulzeitverlängerung von G8 auf G9 (G8=Gymnasium mit nur
acht Jahren von Klasse 5 bis Jahrgangsstufe 12 - statt
früher und jetzt wieder neun Jahre von 5 bis 13). Hier eine
Übersicht über die Pläne aller Fächer
https://www.schulentwicklung.nrw.de/lehrplaene/lehrplannavigator-s-i/gymnasium-aufsteigend-ab-2019-20/index.html
bzw. speziell zur Mathematik https://www.schulentwicklung.nrw.de/lehrplaene/lehrplan/195/g9_m_klp_3401_2019_06_23.pdf
zum Seitenanfang / zum Seitenende
Trigonometrie und
Fotovoltaik
Hier geht es -- ähnlich wie in der weiter
unten bei der Analysis erwähnten Einführung in die
Integralrechnung -- um die Einbindung unserer (damaligen)
Fotovoltaik-Anlage in den (Mathematik-) Unterricht, hier in der
SI. Mehr um Sonnenstrom gibt's auf meiner "Fotovoltaik"-Hauptseite. Den Stundenentwurf für
die 10. Klasse gibt's auf einer
Extra-Seite
Meiner Meinung nach muss man dem
Schülerinnen und Schülern durch geeignete Beispiele und
die vielfältige Erschließung von Alltagssituationen
immer wieder verdeutlichen, wo und wie Mathematik gebraucht wird.
Mathematik in der Schule darf keine abstrakte, unnütze
Wissenschaft bleiben. Wenn die Schülerinnen und
Schülern einen Sinn erkennen, lernen sie leichter, besser
und schneller, was evtl. zusätzlichen Zeitaufwand für
das Mathematisieren der Alltagssituation mehr als wettmacht. Mehr
dazu finden Sie im folgenden Kapitel.
(Natürlich muss insbesondere in der SII gelegentlich auch
dargestellt werden, wie etwa ein Mathematik-Studium an der
Universität aussieht, um Fehlentscheidungen bei der
Studienwahl vorzubeugen).
 zum Seitenanfang / zum Seitenende
zum Seitenanfang / zum Seitenende
Mathematische
Fähigkeiten
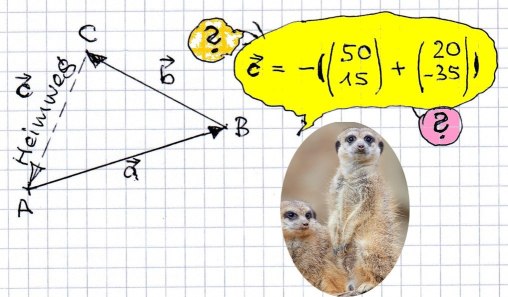 Vor
Längerem habe ich irgendwo mal die Schlagzeile gelesen:
"Erdmännchen können Vektorrechnung!".
Tatsächlich hatte man Erdmännchen in einem neuen,
unübersichtlichen Gelände zur Höhle A gebracht.
Dann wurden sie mit Futter zu einem entfernten Punkt B und
schließlich von dort zum Punkt C gelockt. Nach der
Fütterung hatte man die poussierlichen Tierchen sich
selbst überlassen, die schließlich zur Höhle A
zurück kehrten -- aber überwiegend nicht mit dem
Umweg über B, sondern indem sie einen direkten Weg suchten
und fanden. Allerdings dürfte es etwas übertrieben
sein, hieraus auf die Beherrschung der Vektorrechnung und ein
tiefes Verständnis von Linearer Algebra zu
schließen. Aber die Tiere haben offenbar eine gute
Raumvorstellung bzw. eine 'inneren Karte'.
Vor
Längerem habe ich irgendwo mal die Schlagzeile gelesen:
"Erdmännchen können Vektorrechnung!".
Tatsächlich hatte man Erdmännchen in einem neuen,
unübersichtlichen Gelände zur Höhle A gebracht.
Dann wurden sie mit Futter zu einem entfernten Punkt B und
schließlich von dort zum Punkt C gelockt. Nach der
Fütterung hatte man die poussierlichen Tierchen sich
selbst überlassen, die schließlich zur Höhle A
zurück kehrten -- aber überwiegend nicht mit dem
Umweg über B, sondern indem sie einen direkten Weg suchten
und fanden. Allerdings dürfte es etwas übertrieben
sein, hieraus auf die Beherrschung der Vektorrechnung und ein
tiefes Verständnis von Linearer Algebra zu
schließen. Aber die Tiere haben offenbar eine gute
Raumvorstellung bzw. eine 'inneren Karte'.
- Krähenvögel können zählen (zumindest
bis 4), können geometrische Figuren auf einem Bildschirm
erkennen bzw. unterscheiden ("beherrschen also", wieder in
reißerischer Formulierung, "Arithmetik und Geometrie!")
und können anscheinend vorausschauend planen. Darüber
(und den bekannten Werkzeuggebrauch dieser Vögel)
berichtete z.B. RP-Online im April 2025.
- Homer Simpson aus der Animationsserie "Die Simpsons"
widerlegte schon vor einigen Jahren in einer Folge mal ebenso
nebenher mit Hilfe seines Taschenrechners den großen Satz
von Fermat, indem er die Lösung einer Gleichung vorzeigte,
die zu einer seit 1665 als unlösbar geltenden Sorte von
Gleichungen gehört. Bei genauerem Hinsehen brachte die
Zeichentrickfigur aber nicht die Mathematik zum Wanken, sondern
bewies nur einmal mehr, dass numerisches Rechnen ungenau ist
und der Taschenrechner höchstens auf 11 bis 13 Stellen
genau arbeitet, während im Beispiel für eine exakte
Berechnung (die dann allerdings doch nicht aufgeht) eine
Genauigkeit von mindestens 48 Stellen erforderlich gewesen
wäre. Hintergründe und die verwendeten Zahlen
verrät eine Spektrum-Kolumne.
- Junge Menschen werden durch nur formalen,
herkömmlichen Mathematik-Unterricht nicht ausreichend aufs
Leben vorbereitet, wenn im Unterricht nicht auch immer wieder
der Anwendungsbezug bzw. die Verknüpfung mit der
Lebenswelt hergestellt und geübt wird. Umgekehrt scheitern
arbeitende Kinder ohne Schulbesuch, die in ihrem Alltag z.Z.
beeindruckende Rechenfähigkeiten erworben haben, dabei,
formale Aufgaben über diesen Bereich zu lösen. Eine
entsprechende Studie aus Indien wurde im Februar 2025 in den
Spektrum-News vorgestellt.
In vielen Bundesländern, insbesondere und früh in
Nordrhein-Westfalen (dort u.a. durch die unermüdliche
Arbeit der MUED angeregt - s.u.), ist zum Glück seit
vielen Jahren die Pflicht zu Anwendungsbezügen in die
Mathematik-Lehrpläne und -Abiturvorschriften aufgenommen
worden. Anregungen zur Unterrichtspraxis können im
nachfolgende Abschnitt und bei der MUED gefunden werden
zum Seitenanfang / zum Seitenende
Anwendungsbezug und
Realitätsnähe in der
Mathematik
Wirkliche Anwendungen kommen leider auch heute noch im
Mathematik-Unterricht oft zu kurz. Es reicht nicht, mathematische
Formeln und Verfahren innermathematisch anzuwenden oder
dürftig in kurze Texte einzukleiden, die einen stark
abstrahierten und idealisiert-verkürzten Verweis auf
Alltagsprobleme andeuten. Solches Vorgehen hat in bestimmten
Phasen sicher auch seinen Wert und Platz im Unterricht,
lässt aber einen wichtigen Aspekt außer Acht:
Um Schülerinnen und Schülern den Sinn der Mathematik
klar zu machen und sie zu befähigen, Mathematik selbst im
Alltag anzuwenden - auch dann, wenn zufällig gerade keine
Schulbuchaufgabe am Problem aufgedruckt ist - , ist es
unerlässlich, im Unterricht auch das Mathematisieren und
Abstrahieren selbst immer wieder zu üben. Ausgehend von
offenen alltäglichen Situationen oder Problemen muss das
allmähliche Analysieren, Herausarbeiten sinnvoller
Fragestellungen und mathematische Formalisieren und Bearbeiten
immer wieder durchgeführt und eingeübt werden. Auch
über dabei durchgeführte Vereinfachungen, Annahmen,
Idealisierungen und Grenzen der Modelle und Verfahren muss
nachgedacht und gesprochen werden.
Am besten geschieht dies natürlich mit Handlungsbezug und
in realen Situationen, möglichst aus dem Erfahrungsbereich
der Schülerinnen und Schüler. Problemlagen können
(und müssen) aber auch auf verschiedene Art in den
Unterricht hereingeholt und vorgestellt werden. Die neuen Medien
können dabei helfen, sind aber nicht automatisch Garant
für einen besseren Unterricht oder einen aufrichtigen Zugang
zur Realität. In meinen Rezensionen zur Mathematik-Software
(s.u.) musste ich leider häufig bemängeln, dass dort
herkömmliche Verkürzungen elektronisch fortgeschrieben
werden.
Auf jeden Fall ein deutlicher Schritt in die richtige Richtung
ist hingegen das für den Oberstufen-Unterricht von Willi van
Lück angelegte (inzwischen von Antonius Warmeling betreute)
reichhaltige Webangebot auf dem südtiroler Blikk-Server:
Reale Probleme modellieren mit Mathe
http://www.blikk.it/blikk/angebote/modellmathe/
In Anleitungen für Schüler und Lehrer wird die
sinnvolle Nutzung der Materialien vorgeschlagen. Gedacht ist vor
allem daran, dass neue mathematische Teilgebiete im Unterricht
nicht fachsystematisch durch Entwickeln des mathematischen Kerns
eingeführt werden müssen, sondern Schülerinnen und
Schüler in Kleingruppen den Auftrag erhalten, sich jeweils
aus dem Webangebot ein Problem heraus zu suchen und es zu
bearbeiten. Erst nach dem Vorstellen verschiedener Probleme und
verschiedener Ansätze durch die Gruppen soll dann das
Gemeinsame, der mathematische Gedanke bzw. das neue Verfahren
abstrahiert und formalisiert werden. So wird jedenfalls klar,
wozu das Verfahren gebraucht wird. Und die Lernenden haben die
erste Anwendung dazu schon - medial vermittelt - zumindest
virtuell "erlebt". Stöbern auf diesen Webseiten lohnt auf
jeden Fall!
Nach dem großen Erfolg des gerade vorgestellten
Webangebots "Reale Probleme modellieren mit Mathe" für die
SII wurde von den gleichen Autoren (Willi van Lück, Antonius
Warmeling, Hans Kratz u.a.) eine ähnliche
internet-gestützte Mathe-Umgebung für jüngere
Schülerinnen und Schüler (etwa der Klassen 3 bis 6,
evtl. auch bis Klasse 7) aufgebaut. Auch hier lohnt das
Reinschauen sowie das Lesen auch in den Handreichungen und
pädagogischen Kommentaren und natürlich das Arbeiten
mit dem bereitgestellten Material:
Mathe
Überall (f. Klassen 3 bis
7)
http://www.blikk.it/angebote/primarmathe/
(Weitere Hinweise sowie Links zum Einsatz neuer Medien, auch
in http://www.blikk.it/angebote/schulegestalten/neuemedien/infothek.htm.)
Auch die Seite des Lehrers Werner Brefeld,
Mathematik - Hintergründe im täglichen
Leben
nennt Beispiele echter Anwendungen der Mathematik. Anders als
bei den vorgenannten südtiroler Seiten ist hier allerdings
der Schritt von der komplexen Anwendungssituation hin zur
schulbuchaufgaben-ähnlichen, mathematischen Beschreibung
meist schon getan (was allerdings nach manchem eher
traditionellem Unterricht den Einstieg vielleicht vereinfacht und
so dann auch Mut zu Behandlung von Problemen aus realistischeren
Zusammenhängen macht).
Die gut gemeinten Aktionen zum Jahr der Mathematik 2008 (s.u.)
hatten leider noch nicht die Breitenwirkung, um die
Lebensnähe der Mathematik mehr ins Bewusstsein zu
rücken!
Auf dem auf dem nordrhein-westfälischen Bildungsserver
Learn:Line wurde früher auch Mal "in einer Ecke"
realitätsbezogeneres Material gesammelt. Inzwischen wurde
der Webauftritt neu organisiert und wird jetzt vom
Schulministerium betrieben. Zunächst muss man auf
http://www.learnline.schulministerium.nrw.de/suche/Mathematik
den Ort des nächsten Medienzentrums wählen. Sucht
man dann nach "Mathematik", werden z.B. für Düsseldorf
über 3300 Treffer gemeldet. Zum Glück müssen nicht
alle durchgeblättert werden; die Suche kann nach Medientyp
oder nach Schlüsselwörtern verfeinert werden
(außerdem lassen sich dort oben statt einfach nur
"Mathematik" auch noch "angewandte Mathematik" oder auch
"entdeckendes Lernen" mit Bildungsbereich und Fächern
eingeben).
zum Seitenanfang / zum Seitenende
MUED e.V.
Die MUED ist ein Verein engagierter Mathematik-Lehrerinnen und
-Lehrer aller Bundesländer und Schulformen. Ziel ist es,
beziehungshaltigen, realitätsnahen Unterricht zu gestalten
und Schülerinnen und Schüler als Menschen Ernst zu
nehmen (und die Lerninhalte und -formen entsprechend zu
wählen). Statt Mathematik an trockenen Buchaufgaben zu
üben, sollen möglichst echte, sinnvolle Beispiele
verwendet werden. Der zusätzliche Nebeneffekt, dass
Schülerinnen und Schüler dadurch außer Mathematik
auch noch etwas über den behandelten Gegenstand lernen, ist
gewollt. Leider ist es bei der Unterrichts-Vorbereitung nicht
immer leicht, relevante Informationen zu beschaffen (woran die
Schülerinnen und Schüler übrigens beteiligt werden
können und sollen!). Deswegen werden erstellte
Arbeitsmaterialen und Erfahrungen untereinander ausgetauscht bzw.
arbeiten einige Lehrerinnen und Lehrer ihre Materialien
dankenswerterweise soweit aus, dass sie aus einem
Mitglieder-Bereich des Internets herunter geladen und verwendet
werden können oder sogar in Buch- oder Broschüren-Form
allgemein gekauft werden können. Inzwischen sind viele
Hunderte, wenn nicht gar Tausende dieser so genannten
Unterrichtseinheiten verfügbar; eine ganze Reihe von
Freiwilligen (die allerdings durchaus noch Verstärkung
brauchen könnten) arbeitet daran, auch ältere Einheiten
immer wieder zu prüfen und auf den aktuellen Stand zu
bringen und die Kataloge zu aktualisieren. Wegen der früher
einmal auf Papier in großen Karteikästen bereit
gehaltenen Unterrichtseinheiten hatte der Verein den Namen
"Mathematik-UnterrichtsEinheiten-Datei" angenommen, der heute
vielleicht etwas unglücklich wirkt. Aber es kommt ja nicht
auf den Namen, sondern auf den Inhalt bzw. auf die Leistung
an!
Die MUED-Zentrale ist 2019 von Appelhülsen nach
Münster umgezogen und hat seither die Adresse
MUED e.V.
Windthorststr. 7, 48143 Münster
Die MUED hat in den letzen Jahrzehnten spürbar positiven
Einfluss auf die Aufgabenkultur insbesondere in
Nordrhein-Westfalen, aber auch in anderen Bundesländern
nehmen können. Sie tritt auf vielen Bildungsmessen mit einem
Stand auf; ihre Mitglieder oder von ihr beeinflusste Didaktiker
und Autoren veröffentlichen immer wieder in
Fachzeitschriften für Schulmathematik. Der Verein
veranstaltet jährlich zwei Tagungen, wobei insbesondere die
große Herbsttagung mit spannenden Vorträgen und
Mitmach-Arbeitsgruppen als lohnende Fortbildung und zum
großen Erfahrungsaustausch und zur gegenseitigen Ermutigung
im Ringen um weitere, sinnhafte Unterrichtsinhalte und geschickte
Aufarbeitung und Vermittlung gestandenen Lehrerinnen und Lehrern
ebenso wie Berufsanfängern sehr zu empfehlen ist.
Ein viermal jährlich erscheinender Rundbrief sowie die
monatlichen, jetzt von verschiedenen Regionalgruppen im Wechsel
vorgestellten 'Arbeitsblätter des Monats' ergänzen das
Angebot.
Der Verein ist unter
https://www.mued.de
im Internet vertreten. Eine erste Annäherung kann z.B.
über das erwähnte jeweilige Arbeitsblatt des Monats erfolgen, das oft aktuelle
Themen behandelt.
zum Seitenanfang / zum Seitenende
Stochastik in Unterricht und
Alltag
Außer in den nachfolgenden Abschnitten
findet sich außerdem viel Stochastik in meinen Klausuren!
Stochastik in der
SII
Weil das Testen von Hypothesen noch nicht in allen
Schulbüchern und Aufgaben völlig korrekt oder
nachvollziehbar behandelt wird, habe ich eine Zusammenfassung zum
Thema verfasst. Ursprünglich war das Blatt für
Mathematik-Lehrerinnen und -Lehrer gedacht und wurde nochmal
etwas verbessert, bleibt aber sehr knapp:
Übersichtsblatt "Richtiges_Hypothesentesten.pdf" (111
kB)
Außerdem finden Sie umfangreiche (meist ältere,
aber noch nicht veraltete) Beiträge und Arbeitsmaterialien
zur Stochastik in der Sekundarstufe II, u.a. zu
- Zählverfahren in der Kombinatorik,
- Einführung der Binomial-Verteilung,
- Macht Mathematik depressiv? (Hypothesentest und
Test-Theorie)
- Macho-Aufgabe in der Mathe-Klassenarbeit
- Von der Binomial- zur Normalverteilung unter Verwendung des
Tabellenkalkulationsprogramms Excel
- TV-Talkshow-Exhibitionismus ausgerechnet (jetzt mit
ausführl. Lösungen)
- Gegen das Zentralabitur (hat aber leider nicht
genützt - Anm. d. Verf.)
zum Ansehen und/oder Herunterladen zusammengefasst in einer
pdf-Datei:
Zur eigenen Berechnung von Tabellen der Binomial-Verteilung
für beliebige n und p gibt's
außerdem eine interaktives Excel-Arbeitsblatt, das nach dem
Herunterladen (Rechtsklick auf den nachfolgenden Link und "Ziel
speichern unter..") natürlich auch mit vielen anderen
Tabellenkalkulationsprogrammen benutzt werden kann, u.a. auch mit
dem kostenlosen Calc von LibreOffice (bzw. von OpenOffice) oder dem
kostenlosen PlanMaker aus dem Gratis-Office-Paket
Softmaker-FreeOffice:
Rechenblatt
"binomialtabelle.xls" (96 kB)
Und Stichprobenergebnisse binomialverteilter
Zufallsgrößen lassen sich - zur Veranschaulichung von
Lieferanten- oder Abnehmerrisiko bzw. der Signifikanz von
Hypothesentests - auf meiner nachfolgenden Extraseite mit
Javascript online zufällig erzeugen bzw. simulieren:
Extraseite: Simulation
von Zufalls-Stichproben
Und natürlich gehören auch die beiden nachfolgenden
Beiträge (und später eine Buchrezension) zur Stochastik
in Sekundarstufe II:
zum Seitenanfang / zum Seitenende
Hypothesentest
paranormaler Fähigkeiten
Am 19. Oktober 2017
hatte ich die Fernsehsendung der Reihe "Planet Wissen" mit dem
Titel "Übersinnliche Phänomene - Was ist dran?"
gesehen, die in mehreren ARD-Programmen, u.a. im WDR,
ausgestrahlt worden war. Nach erneuter Sendung am 16.10.2018 gab
es das Video noch bis Oktober 2023 im Internet. Im Februar 2024
war es aber leider nicht mehr in der Mediathek zu finden.
Offenbar muss man erst auf eine erneute Ausstrahlung
warten.
U.a. wurde dort von
einer Frau berichtet (ab etwa der 51. Minute im Video), die
behauptete, verschmutzte Blumenerde durch Pendeln erkennen zu
können. Sie wollte damit den von der GWUP -- Gesellschaft
zur wissenschaftlichen Untersuchung von Parawissenschaften --
ausgesetzten Preis von 10.000,- € gewinnen, wenn sie ihre
Fähigkeiten unter Laborbedingungen nachweisen
könne.
Sie war mit
folgendem Test einverstanden: Auf letztlich insgesamt 13 langen
Tischen standen in ausreichendem Abstand jeweils 10 Schalen mit
Blumenerde, wobei jeweils genau eine Schale pro Tisch durch
Beimischung von Zucker verunreinigt war. Das Preisgeld sollte
ausgezahlt werden, wenn sie an mindestens 10 der 13 Tische die
Schale mit der verunreinigten Erde richtig identifizieren
könnte.
Die Dame, die von
ihren besonderen Fähigkeiten überzeugt war, lies einen
Gegenstand über den Schalen pendeln und bezeichnete pro
Tisch eine Schale als verunreinigt. Sie war überzeugt, an
allen 13 Tischen die richtige Schale gefunden zu haben.
Tatsächlich hatte sie allerdings nur an zwei Tischen die
verunreinigte Erde gefunden, hielt das aber dann immer noch
für einen Beweis ihrer übersinnlichen Fähigkeiten,
auch wenn sie den Preis nicht gewonnen hatte. Der Versuchsleiter
konnte sie anscheinend nicht wirklich davon überzeugen, dass
jeder beliebige Teilnehmer allein durch zufälliges Raten mit
hoher Wahrscheinlichkeit zwei Treffer erzielt
hätte.
Die GWUP, die
offenbar schon seit Jahrzehnten einmal jährlich in den
Räumen der Uni Würzburg Tests mit Pendlern,
Wünschelrutengängern und weiteren Kandidatinnen und
Kandidaten durchführt, hat übrigens das ausgelobte Geld
noch nie bezahlen müssen: kein selbsternanntes Medium konnte
seine angeblichen Fähigkeiten unter den mit den Kandidaten
abgesprochenen, arrangierten und kontrollierten Bedingungen unter
Beweis stellen.
Insoweit hatte mich
die Fernsehsendung nicht weiter überrascht. Umso erstaunter
war ich, als gegen Ende der Sendung einer der beiden
Studiogäste plötzlich über den Test schimpfte:
Walter von Lucadou, Leiter der Parapsychologischen
Beratungsstelle in Freiburg, behauptete unvermittelt und ohne
weitere Erklärung, einen solchen Test könne niemand
bestehen, und es sei unethisch, die naive Teilnehmerin, die keine
Ahnung von Stochastik habe, so vorzuführen (etwa in der 55.
Minute des Videos)
Im Fernsehbericht
hatte sich aber bis dahin niemand über die Pendlerin lustig
gemacht oder abfällig über sie gesprochen. Nur Herr von
Lucadou bezeichnete sie jetzt öffentlich als naiv. Wer an
einem solchen Test teilnimmt, um Geld zu gewinnen und seine
behaupteten Fähigkeiten zu demonstrieren, und sich mit den
Versuchsbedingungen einverstanden erklärt hat, muss meiner
Meinung nach auch hinnehmen, dass sachlich über eine
eventuelle Niederlage berichtet wird. Jeder Sportler im Wettkampf
muss von Fans und Berichterstattung weit Schlimmeres ertragen.
Die Teilnehmerin muss auch keinen Stochastikkurs absolviert
haben, um behaupten zu können, dass sie alle dreizehn (auf
jeden Fall aber mindestens zehn) Tische richtig bewerten
könne. Der Vorwurf, ein solcher Test sei viel zu hart, um
bestanden werden zu können, erschien mir auf Anhieb
ebenfalls ungerechtfertigt, blieb aber im Gedächtnis und
regte mich nachträglich zu folgendem Nachrechnen
an:
Entsprechend ihrer
eigenen Behauptung muss man von der Vermutung H1
ausgehen, die Teilnehmerin verfüge über besondere
("paranormale") Erkenntnismöglichkeiten (ihre Erkenntnisrate
p sei also höher als eine willkürlich gesetzte Grenze
p0, d.h.
H1: p > p0). Entsprechend
muss man versuchen, zum Beweis von H1 das Gegenteil,
nämlich die Nullhypothese H0: p <=
p0 zu widerlegen. Geht man - mangels mitgeteilter
Informationen - davon aus, dass auch hier mit der oft
üblichen Irrtumswahrscheinlichkeit von
alpha <= 5 % für den maximalen Fehler 1.
Art gearbeitet wird, und die Entscheidungsregel ja bekannt ist
(Preisgeld und damit Ablehnung von H0 bei 10 bis 13
richtigen Tischen, sonst - bei 0 bis 9 Richtigen - kein Preis
bzw. Vereinbarkeit mit H0), so sollte sich
p0 aus der aufsummierten Binomialverteilung ermitteln
lassen, weil
(*) Bn,p,k(13; p0; 10..13)
= P (X <= 13) - P (X <= 9)
<= 0,05 = 5 %
gefordert ist. Mit
einem modernen Taschenrechner oder auch durch Probieren (also
Einsetzen verschiedener p-Werte) z.B. in meinem Rechenblatt
"binomialtabelle.xls" (weiter oben auf dieser Seite) findet man,
dass bei p0 = 0,5 die Bedingung (*)
erfüllt ist (bei p0 = 0,51 hingegen
nicht mehr):
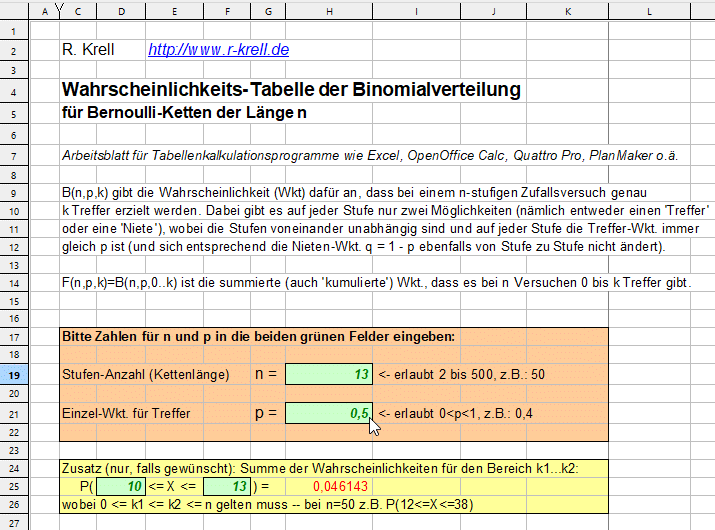
Die GWUP verteilt das Preisgeld also im Prinzip schon, wenn die
Pendlerin erkennbar mindestens die Hälfte der Tische richtig
beurteilt. Wegen der unvermeidlichen zufälligen
Ergebnis-Abweichungen bei kleinen Versuchs- bzw. Tischzahlen
reicht es aber nicht, etwa auf 7 (nächste ganze Zahl
über dem Erwartungswert von 6,5 = 0,5 * 13)
Tischen die Schale mit der verunreinigten Erde genau zu
lokalisieren. Erst bei 10 richtig gelösten Tischen liegt das
Ergebnis soweit über dem zufälligen
‚statistischen Rauschen', dass die 10.000 €
ausgezahlt werden sollen - obwohl auch bei dieser
Entscheidungsregel noch in rund einem von zwanzig Tests
(5 %) die Prämie insofern zu Unrecht gewährt
würde, weil das gute Abschneiden eben doch nur durch
glücklichen Zufall von einem Kandidaten mit in Wirklichkeit
unter 50 % Erkennungsrate bei den Tischen erreicht
wird.
50 % richtige
Tische zu fordern, erscheint auf den ersten Blick sehr fair.
Andererseits soll nicht vergessen werden, dass auf einem Tisch
nicht etwa nur zwei, sondern zehn Schalen stehen. Die Chance,
durch reinen Zufall einen ganzen Tisch richtig zu beurteilen,
liegt also nicht bei 50 %, sondern nur
bei 10 %!
Und um 10 von 13
Tischen richtig zu beurteilen, müsste der einzelne Tisch
auch nicht mit 50 %, sondern mit einer Sicherheit von
76,9 % richtig erkannt werden (erst dann liegt der
Erwartungswert bei 10 Tischen) - also 7,7 mal besser als beim
unbedarften Raten. Und selbst für ein Medium mit 76,9-%-iger
Tischerkennung ist das Risiko 2. Art mit etwa 35 % recht
hoch und 7 mal so groß wie das Risiko 1. Art. Das ist
ungünstig für den Kandidaten.
(Zur Erinnerung:
Ein Fehler 2. Art entstünde, wenn durch ein
zufällig schlechtes Stichprobenergebnis ein in Wirklichkeit
fähiges Medium fälschlich nicht als solches erkannt
würde. Das Risiko 2. Art wäre die Wahrscheinlichkeit
für das Auftreten des Fehlers 2. Art beim Test. - Beim
Fehler 1. Art wird hier hingegen ein schlechtes Medium wegen
zufällig gutem Stichprobenergebnis/glücklichem Raten
irrtümlich für eine Person mit besonderer Begabung
gehalten. Die Wahrscheinlichkeit hierfür ist das Risiko 1.
Art, auch Irrtumswahrscheinlichkeit genannt).
Legt man das
Anforderungsniveau für Abiturnoten in NRW zu Grunde,
müsste die Pendlerin für 76,9-%-ige Tischerkennung also
schon "gut" sein, um den Preis zu erreichen (ab 75 % der
Rohpunkte soll es für eine Abiturarbeit eine glatte Zwei
geben; ab 80 % gibt es eine Zweiplus, ab 85 % eine
Einsminus usw.). Einer Person mit nur "ausreichenden" oder
"befriedigenden" besonderen Eigenschaften will die GWUP die
ausgelobten 10.000 € offenbar möglichst nicht zahlen.
Liegt hier der Grund für die abfällige
Äußerung seitens Herrn von Lucadou? Wenn er den Test
als überzogen und als nicht bestehbar verdammt, geht er wohl
davon aus, dass es keine Personen mit guten paranormalen
Fähigkeiten gibt - wer wollte da widersprechen.
Die Freiburger
Beratungsstelle zeigt sich sonst allerdings nicht so skeptisch:
nach eigenen Angaben erreichen sie pro Jahr einige Tausend Anrufe
von Leuten, die vor allem nicht für verrückt gehalten
werden wollen, weil sie für sie unerklärliche
Phänomene beobachtet haben. Dr. Dr. von Lucadou, der nicht
nur in Physik, sondern auch in Psychologie promoviert hat, nimmt
diese Anrufer ernst, hört ihnen unvoreingenommen zu und
beruhigt, dass auch andere Ähnliches erlebt hätten.
Auch wenn im weit überwiegenden Teil der geschilderten
Fälle bald natürliche Erklärungen gefunden werden,
bleibt wohl ein kleiner Prozentsatz, wo dies nicht gelingt. Herr
von Lucadou berichtet von spukhaften Ereignissen, die zwar
abgestellt (weil Lebensbedingungen verändert oder
uneingestandene Wünsche erkannt und beachtet wurden), aber
nicht wirklich erklärt werden konnten. Letzteres sei
allerdings auch nicht sein Ziel; vielmehr gehe es darum, den
Anrufern zu helfen. Und solange man noch nicht genau wisse, durch
welchen exakten physikalischen Mechanismus bei psychosomatischen
Krankheiten z.B. negative Gedanken ein Magengeschwür im
eigenen Körper verursachen können, hält er es auch
für möglich, dass Gedanken sogar nach außen
wirken. Die von ihm nebulös verwendeten Begriffe der
Verschränkung (der in der Physik allerdings nur bei Paaren
isolierter Elementarteilchen unter ganz bestimmten Bedingungen
vorkommt) und der Musterübereinstimmung überzeugen
nicht wirklich und ersetzen keine fehlende Erklärung. Hier
wird meiner Meinung nach der von ihm erhobene
naturwissenschaftliche Anspruch klar verlassen.
Die GWUP
veranstaltet die jährlichen Tests übrigens, um zu
zeigen, dass es keine paranormalen Fähigkeiten gibt (auch
wenn viele der Kandidaten sich für übersinnlich begabt
halten - es aber unter Testbedingungen nie nachweisen konnten).
Ab welcher ‚Qualität' die GWUP einen Preis anbietet,
bleibt ihr natürlich überlassen. Und eine Kandidatin,
die bis zum Schluss des Tests zu 100 % überzeugt war,
alle 13 Tische richtig erkannt zu haben, weil sie ja klare
Signale beim Pendeln erfahren habe, hätte sicher auch am
Test teilgenommen, wenn sie die vorstehende Rechnung
durchgeführt und von der 76,9-%-Marke gewusst
hätte.
Zur Abrundung noch
die zu erwartende Tischzahl für den völlig unbegabten
Rater (der blind auf eines der 10 Schälchen pro Tisch tippt
und damit nur eine 10-%-ige Chance auf eine richtige
Tischerkennung hat): Der Erwartungswert liegt dann wegen
0,1 * 13 = 1,3 bei 1,3 richtig geratenen Tischen -
wobei natürlich kein Tisch zu einem Bruchteil richtig sein
kann, sondern nur ganze Zahlen als Ergebnisse möglich sind.
Wegen
Bn,p,k (13; 0,1; 1) = 0,3672
und Bn,p,k (13; 0,1; 2) = 0,2448
liegt die Wahrscheinlichkeit, bei zufälligem Raten 1 bis 2
Tische richtig zu haben, bei über 61 %. Nur in einem
Viertel der Fälle (25,4 %) wird ein ratender Laie gar
keinen richtigen Tisch benennen können. Will man
zufälliges Raten mit höchstens 5-%-iger
Irrtumswahrscheinlichkeit ausschließen, darf dies erst ab 4
(bis 13) richtig geratenen Tischen passieren. Die 2 von der
Kandidatin im Film richtig erpendelten Tische ergeben also
wirklich keinerlei Hinweis auf besondere
Fähigkeiten!
Quellen und
Verweise / Links
- Sendung "Planet
Wissen: Übersinnliche Fähigkeiten - Was ist dran?",
erstmals gesendet von WDR, SWR und ARD-alpha am 19.10.2017, mit
Moderator Jo Hiller und den Studiogästen Thorsten Havener
und Walter von Lucadou. Leider wird auf der
Planet-Wissen-Webseite die Verlinkung der Beiträge
häufig geändert. Das 58-min-Video war bis Oktober
2023 abrufbar und wurde im Februar 2025 von mir leider nicht
mehr gefunden..
- Gesellschaft zur
wissenschaftlichen Untersuchung von Parawissenschaften (GWUP)
in Würzburg: www.gwup.org
- Parapsychologische
Beratungsstelle in Freiburg: www.parapsychologische-beratungsstelle.de
- Mehrere Videos zum Thema "Geister und Grusel" gibt es auf
planet-wissen.
Das Video "1 Minute mit Walter von Lucadou,.." scheint
aber auch verschwunden. Achtung: Verlinkung kann sich
ändern; Beiträge werden häufig ausgetauscht -
einfach selbst auf Planet Wissen suchen!
- Auf RTL+ gibt es
inzwischen aber offenbar eine (vermutlich nicht allzu
seriöse) Serie "Dr. von Lucadou und die unheimlichen
Fälle"; auf Youtube findet man ein über
einstündiges Gespräch "Paranormale Phänomen physikalisch
erklärt". Das Schweizer Radio und Fernsehen (SRF)
präsentiert auf seiner Webseite noch einen Artikel vom Juli 2022 mit Videos von und
über Lucadou -- und auch Wikipedia kennt den Parapsychologen, der
allerdings seit 2019 mit dem Land Baden-Württemberg
überkreuz liegt (wie der focus 2022 berichtete).
- Tabellenblatt
zur Berechnung binomialverteilter Wahrscheinlichkeiten
"binomialtabelle.xls" weiter oben auf
diese Seite
- Weitere Hinweise
zur Testtheorie
- in meinem
pdf-Dokument "Stochastik in der SII" (stoch_s2.pdf),
erreichbar weiter oben auf diese
Seite
- in meiner
Zusammenfassung "Richtiges_Hypothesentesten.pdf" weiter oben auf diese Seite
- bei meiner
3. Buchbesprechung "Stochastik-Fehler" weiter unten auf dieser Seite
- im
nachfolgenden Artikel "Wissenschaftskrise .. wegen
falschverstandener Hypothesentests" etwas weiter unten auf dieser Seite
- in meinem
Artikel "Fachleute leiten aus gleichen Daten
widersprüchliche Ergebnisse ab" weiter unten auf dieser Seite
- in mehreren
Klausuren zur Stochastik bei meinen Mathematik-Klausuren (dort bitte die
Lösungen beachten!)
Weiterführende
Aufgaben
- Rechne nach,
dass - wie im letzten Absatz des vorstehenden Textes angegeben
- beim einseitigen Test erst bei 4 und mehr richtig geratenen
Tischen (à 10 Schalen, von denen genau eine
verunreinigte Erde enthält) eine signifikante Abweichung
vom zufällig zu erwartenden Ergebnis vorliegt, sodass mit
alpha = 5 % Irrtumswahrscheinlichkeit eine
besondere Fähigkeit attestiert wird. Begründe auch,
warum nicht zweiseitig getestet wird.
- Führe die
Rechnung von 1. für eine Irrtumswahrscheinlichkeit von nur
1 % durch.
- Nimm an, das
Preisgeld würde schon bei 8 (und mehr) richtig geratenen
Tischen ausgezahlt. Welches p0 wird dann
gefordert?
- Jetzt soll das
Preisgeld schon ausgezahlt werden, wenn H0: p <=
0,2 widerlegt werden kann (der Kandidat also signifikant mehr
als doppelt so gut wie ein zufälliger Rater sein soll).
Stelle die Entscheidungsregel für
alpha = 5 % auf und bestimme den Fehler 2. Art
für ein hypothetisches Medium, das in Wirklichkeit bzw.
auf lange Sicht a) 40 %, b) 50 %,
c) 76,9 % der Tische richtig erkennen
kann.
- Nimm für
einen Moment an, es gäbe wirklich Personen mit
paranormalen Fähigkeiten, die im Mittel 20 % (oder
mehr) der Tische richtig erkennen könnten. Der
Stichprobenumfang sei wieder n=13, d.h. jede Person soll wieder
13 Tische bewerten. Danach muss entschieden werden, ob die
Person ein begabtes Medium oder ein blind ratender Scharlatan
ist. Formuliere die Hypothesen und finde die Entscheidungsregel
so, dass ein solches Medium höchstens mit einer
Irrtumswahrscheinlichkeit von 5 % für einen
Scharlatan gehalten wird. Ermittle auch den Fehler 2. Art, dass
bei diesem Test ein wirklicher Scharlatan als vermeintliches
Medium mit paranormalen Fähigkeiten
durchgeht.
- Die
GWUP-Bedingung, dass pro Tisch genau eine Schale verunreinigt
ist, macht es den Kandidaten eigentlich sogar sehr leicht:
Glaubt beispielsweise ein Kandidat, bei verunreinigter Erde
mache das Pendel eine Kreisbewegung, während es sonst in
einer Ebene schwingt, so kann er, selbst wenn das Pendel
gelegentlich elliptisch schwingt, einfach die Schale mit der
rundesten Ellipse aussuchen, um auf die verunreinigte Schale zu
tippen. Außerhalb des Labors und des GWUP-Tests
weiß man aber nicht, wo wie viel verunreinigte Erde ist.
Ein realitätsnaher Test müsste daher eigentlich pro
Tisch eine beliebige, unbekannte Anzahl an Schälchen
verunreinigen dürfen, was den Test allerdings wesentlich
erschwert. Ermittle, mit welcher Sicherheit dann jede einzelne
Schale richtig erkannt werden muss, damit im Mittel 20 %
aller Tische richtig erkannt werden
können.
- Die Probleme
beim Hypothesentest liegen bekanntlich nicht in der Mathematik,
sondern in den vorher getroffenen willkürlichen
Festsetzungen. Gehe wieder vom einfachen Test mit genau einer
verunreinigten von 10 Schalen pro Tisch aus, und lege
p0 und/oder alpha sinnvoll fest:
Diskutiere und begründe, ab welcher Prozentzahl
p0 für einen richtig erkannten Tisch ein
Kandidat deiner Meinung nach als Medium mit besonderen
Fähigkeiten anerkannt werden sollte und welche
Irrtumswahrscheinlichkeit sinnvoll ist, wenn es
a) ‚nur' um ein Preisgeld von 10.000 €
geht, b) wenn die Kandidatin ihr Geld damit verdient,
gutgläubigen Bauherren zum Kauf eines Grundstücks
(auch auf einem ehemaligen Deponie-Gelände) zu raten / vom
Kauf eines Grundstücks abzuraten / zu einem Umzug zu
raten, wenn der Boden ihrer Meinung nach nicht verseucht bzw.
verseucht ist, c) wenn der Kandidat für seine nicht
verunreinigte Erde besondere heilerische Fähigkeiten
behauptet und man befürchten muss, dass ihm im Falle
seiner Anerkennung möglicherweise weitere Hunderte
Patienten vertrauen, ihm in der Hoffnung auf Heilung ihr
Erspartes für ein Schälchen heilende Erde opfern und
auf das rechtzeitige Aufsuchen eines normalen Arztes
verzichten.
[Den
vorstehenden Beitrag "Hypothesentest paranormaler
Fähigkeiten" gibt's hier auch zum Download in einer pdf-Datei (134 kB) bzw. sogar komplett mit Lösungen (156 kB) -
Achtung: die dort noch angegebenen Verweise auf die
Planet-Wissen-Seite haben sich zwischenzeitlich verändert,
s.o. Außerdem fehlen die Minutenangaben für die
erwähnten Sequenzen innerhalb des Videos]
zum Seitenanfang / zum Seitenende
Wissenschaftskrise u.a. wegen
falschverstandener Hypothesentests
Im Oktober-Heft 2020 berichtet Spektrum der Wissenschaft im
Artikel "Metaforschung - Kulturwandel in der Biomedizin"
ausführlich darüber, dass sehr viele - nämlich
weit mehr als die Hälfte! - der in den letzten Jahren
veröffentlichten biomedizinischen Studien unzuverlässig
und ihre Ergebnisse nicht reproduzierbar sind. Auch in anderen
Fachbereichen sind die Forschungen nicht viel besser; am besten
schnitten Physik und Ingenieurwissenschaften ab. Laut Bericht ist
neben bewusster oder unbewusster Beeinflussung der Messungen vor
allem die Statistik ein großes Problem: Stochastik wird
überwiegend falsch verwendet und ihre Aussagen können
nicht richtig interpretiert werden!
Wenn bei einem Signifikanztest (Hypothesentest) 5%
Irrtumswahrscheinlichkeit festgelegt werden, glauben fast alle
Forscher, wäre das Ergebnis zu 95% sicher. Die 5 % beziehen
sich aber -- wie Leserinnen und Leser der vorstehenden
Beiträge hier auf dieser Seite wissen -- nur auf den Fehler
1. Art, d.h. die irrtümliche Ablehnung der getesteten
Hypothese H. Wurde der Test richtig aufgebaut, ist die Hypothese
H aber nicht die ursprüngliche Vermutung, sondern deren
Gegenteil, nämlich die Gegen- oder Nullhypothese
Ho. Dann bestätigt die Ablehnung von
Ho die ursprüngliche Vermutung, d.h. die zu
überprüfende Aussage. Eine irrtümliche Ablehnung
von Ho führt damit zu einem falsch-positiven
Ergebnis für die Vermutung, die beim Test mit der
Gegenhypothese Ho tatsächlich recht selten
wäre (<= 5%). Allerdings wird im vorgestellten
Zeitschriften-Artikel mitgeteilt: "Hier regt sich ebenfalls
Kritik, denn mehr als 95 Prozent aller Studien bestätigen
die untersuchte Hypothese" (Spektrum der Wissenschaft, Heft
10.20, S. 41). Das ist nur möglich, wenn gar nicht
Ho, sondern fälschlich direkt die Vermutung
getestet wurde - und eine Nichtablehnung als eine
Bestätigung aufgefasst wird (was ebenfalls nicht stimmt,
weil ein positiver Ausgang die Hypothese zwar für
möglich hält, aber nicht wirklich bestätigt - auch
das Gegenteil ist weiterhin möglich). Hier müsste dann
mit dem Fehler 2. Art gerechnet werden. Sein Risiko ist i.A.
schwer zu beziffern, weil man die wahre Wahrscheinlichkeit kennen
müsste. Insbesondere, wenn diese nahe bei der getesteten
Wahrscheinlichkeit liegt und die Stichprobe klein ist,
können (trotz des 5%-Signifikanzniveaus für das Risiko
1. Art) hier aber riesige Fehler-Wahrscheinlichkeiten durchaus
von 80 bis 90% und noch höher entstehen - der Artikel
spricht statt vom Risiko 2. Art von der 'Power' eines Tests und
merkt an: "Befragungen von Studenten, jungen Wissenschaftlern und
sogar gestandenen Professoren haben gezeigt, dass den meisten
Forschern die Bedeutung dieses Umstands gar nicht bewusst ist."
(a.a.O, S. 41).
Außerdem führt die leider immer noch verbreitete
Ansicht, dass nur positive Ergebnisse eine Veröffentlichung
lohnen, dazu, dass viele negative Ergebnisse gar nicht bekannt
gegeben werden und so die publizierten Ergebnisse
überwiegend aus zufälligen positiven Ausreißern
bestehen. Seit Jahrzehnten wird ein Umdenken gefordert. Im
Artikel werden neue 'Belohnungssyteme' für Wissenschaftler
gefordert, sodass nicht mehr die Zahl der (eben leider oft
fragwürdigen) Publikationen karrierefördernd sein soll.
Und durch Voranmeldung von Tests sollen Versuchsbedingungen und
richtiger Testaufbau vorab geprüft werden können und
auch negative Ergebnisse erfasst werden. Sollte beispielsweise
eine korrekt durchgeführte Untersuchung zeigen, dass ein
grüner Webseitenhintergrund bei mathematischen Themen
keineswegs zur Beruhigung beiträgt oder das Wohlbefinden
fördert, müssten nicht Jahr für Jahr
Nachwuchsforscher immer wieder die Vermutung "grün beruhigt"
überprüfen. Selbst bei richtigem Testaufbau würde
trotzdem noch jeder zwanzigste (<= 5%) die Vermutung
zufällig (aber irrtümlich) bestätigen und sein
Ergebnis veröffentlichen, sodass ein interessierter Autor
bei ausgedehnter Recherche auf mehrere solcher Bestätigungen
stoßen würde - während die anderen den wahren
Sachverhalt nicht veröffentlicht haben und so die
Veröffentlichungen ein ganz falsches Bild ergeben
("Publikations-Bias").
Den vollständigen Spektrum-Artikel, aus dem ich zitiert
habe, gibt es online nur kostenpflichtig (hier der Anfang); die wesentlichen Ideen sind
aber schon in einem 14-minütigen Podcast vom Februar 2020
gratis zu hören. Das Thema ist nicht neu: 2005 hatte der
Epidemiologe John Johannides mit seiner These aufgeschreckt, dass
die meisten publizierten Forschungsergebnisse (der Medizin und
verwandter Wissenschaften) falsch seien
[Nachtrag im Mai 2021: Bedauerlicherweise ist J.
Johannidis in jüngster Zeit aber auch unrühmlich
aufgetreten -- als Corona-Leugner und Verharmloser von in
Wirklichkeit eindeutigen Statistiken. Das berichtet z.B. die
FAZ].
Und die beiden deutschen Biophysiker Beck-Bornholt und Dubben
versuchen seit 1998 mit drei sehr lesenswerten und gut
verständlichen Taschenbüchern den richtigen Umgang mit
der Stochastik anschaulich zu erläutern und Fallstricke
aufzuzeigen.
Die Probleme des Publikations-Bias und falscher
Testgläubigkeit war aber schon zu meiner Studienzeit in den
1970er Jahren unter Mathematik-Student(inn)en bekannt, die sich
über die psychologischen Versuche im benachbarten
Fachbereich lustig gemacht haben (obwohl sie sich gegen Bezahlung
gerne als Probanden zur Verfügung gestellt haben). Dort
wurden z.B. beim Test der Vermutung "Mozart-Musik nimmt die Angst
vorm Zahnarzt" möglichst viele Eigenschaften der paar
Probanden erfasst und mit Computerprogrammen (damals noch am
Großrechner) so lange ausgewertet, bis selbst beim
negativen Ergebnis für die ursprüngliche Vermutung
irgendein zufälliger positiver Zusammenhang gefunden werden
konnte, und sei es "Mozart-Musik hilft Menschen mit
Schuhgröße 44, die gerne blaue Pullover tragen, gegen
die Angst vorm Zahnarzt". Ließ sich partout nichts
Signifikantes mit Mozart finden, reichte es vielleicht zu einem
bemerkenswerten Zusammenhang zwischen der Vorliebe für blaue
Pullover und der Schuhgröße (oder anderen
'signifikanten' Korrelationen zwischen vorsorglich erfassten
Eigenschaften). Bei richtigem Testverständnis hätte die
neue Vermutung jetzt in einem neuen Test an neuen Probanden und
mit korrekter Null- bzw. Gegenhypothese getestet werden
müssen. Tatsächlich konnte die Behauptung aber ohne
Überprüfung abgegeben werden und wurde vom Professor
oder der Professorin akzeptiert und honoriert. Studenten, die
zutreffend behaupteten, man müsse vielleicht wo anders
suchen, 'Mozart bringe es jedenfalls nicht', wurden hingegen
aufgefordert, sich endlich anzustrengen und einen positiven
Beitrag zur Wissenschaft zu leisten. Offenbar hat sich an diesem
Unverstand trotz vieler Mahnungen noch nicht viel geändert.
Vielleicht hilft der angesprochene Artikel - wahrscheinlich sind
aber noch viele weitere stete Tropfen nötig, um den Stein zu
höhlen bzw. den beschworenen Kulturwandel endlich herbei zu
führen.
Zusatz im Januar 2022: Erst jetzt stieß ich auf
einen weiteren (Online-)Artikel von Spektrum der Wissenschaft von
2019, der darüber berichtet, dass außerdem in
amerikanischen Universitäts-Lehrbüchern die
statistische Signifikanz oft falsch erklärt wird bzw.
zumindest die Wahrscheinlichkeiten häufig falsch
interpretiert werden. Eigene Erfahrungen mit deutschen
Mathematik-Schulbüchern zeigten auch hier ähnlichen
Verbesserungsbedarf.
Ebenfalls zum Thema passt die Buchrezension von "Statistics
done wrong - Deutsche Ausgabe: Statistik richtig anwenden und
Fehler vermeiden" weiter unten auf dieser
Seite.
zum Seitenanfang / zum Seitenende
Fachleute leiten
aus gleichen Daten
widersprüchliche Aussagen ab
Falsch angewandte Stochastik ist weiterhin ein Problem. Im
Juli 2025 wurde bekannt, dass weltweit 146 Teams von
Ökologen an Universitäten und Forschungseinrichtungen
exakt gleiche Daten erhielten, mit der Bitte, mit ihren
Programmen und Methoden festzustellen, ob Eukalyptus auf
grasbedecktem Boden besser wächst oder nicht. Die in 18
verschiedenen Untersuchungsgebieten in Australien erhobenen Daten
enthielten dabei umfangreiche Informationen zu recht vielen
Aspekten, auch zur Temperatur bzw. weiteren Wetterbedingungen,
Boden- und Pflanzenarten, Fauna usw., deren Relevanz für die
Fragestellung nicht immer offensichtlich war. Das Vorgehen
entspricht der schon oben von mir kritisch beschriebenen
Gepflogenheit vieler Wissenschaftler, möglichst viel zu
erheben, um wenigstens irgendeinen vermeintlichen Zusammenhang
finden zu können, der sich als signifikant ausgeben
lässt.
Überraschenderweise kamen die Analyseteams trotz gleicher
Daten zu unterschiedlichen Ergebnissen: Viele fanden keinen
signifikanten Zusammenhang, andere 'bewiesen', dass Gras dem
Eukalyptus hilft, während wieder andere aus denselben Daten
lasen, dass viel Gras auf dem Boden das Eukalyptus-Wachstum
signifikant behindert. Entscheidend für die Unterschiede war
offenbar die Auswahl der Aspekte, die in die jeweilige Analyse
tatsächlich einbezogen wurden - ob man beispielsweise
erkannte (und glaubte), dass bei höheren Temperaturen und
viel Feuchtigkeit sowohl Gras als auch (wenn auch etwas weniger
stark) Eukalyptus besser wachsen, ohne dass deshalb viel Gras die
Ursache für mehr Eukalyptus sein muss. Beschränkte man
sich hingegen nur auf die Gras- und Eukalyptuswerte unter sonst
möglichst gleichen Bedingungen, traten in der nun viel
kleineren Stichprobe möglicherweise andere
Zufälligkeiten stärker in den Vordergrund und
führten zu abweichenden Ergebnissen. Eventuell gab es auch
hierfür andere, echte Ursachen, die in den vielen z.T.
wahllos gesammelten Daten aber nicht enthalten waren oder von
einigen Analyseteams unentdeckt geblieben sind.
Der Bericht des Journalisten Chr. Schwägerl im Juli-Heft
von "Spektrum der Wissenschaft" (Heft 7.25,
Seiten 68 bis 73) zur Replikationskrise der Ergebnisse wurde mit
"Statistik | Test nicht bestanden" betitelt. Dabei wird
ärgerlicherweise völlig übersehen, dass alle
Analyseergebnisse gar keine Testergebnisse sind und per se nicht
signifikant sein können, sondern allenfalls zu Vermutungen
führen dürfen, die in jedem Fall erst noch in einem
zweiten Schritt an neuen, anderen Daten getestet werden
müssen! Erst danach kann man von Testergebnissen sprechen -
vgl. mein Übersichtsblatt "Richtiges_Hypothesentesten.pdf" (111
kB) weiter oben bei "Stochastik in der
SII".
Wenn also der Bericht über die Multi-Analysten-Studie
selbst wieder nicht klar und präzise formuliert ist, erkennt
man einmal mehr, dass im Umgang mit Statistik noch Vieles im
Argen liegt. Im Zeitschriftenartikel -- der auch noch eine
Untersuchung über Blaumeisen sowie Ideen zu Ursachen und
möglichen Abhilfen für der Fehlanwendung der Stochastik
beinhaltet -- wird der Biologe Hartig zitiert, der offenbar von
den erschreckenden Widersprüchen auch nicht sonderlich
überrascht ist: "Also wenn einen das besorgt, dann hat man
vorher stark die Augen zugemacht".
Hier sei noch eine Anekdote angeführt: Bei meinem
jugendlichen Erstkontakt mit statistischen 'Beweisen' hatte mich
die Tatsache überrascht, dass Menschen, die
Kopfschmerzmittel nehmen, mehr Kopfschmerzen haben als Menschen
ohne Medikamenten-Einnahme. Was zunächst wie eine
kontra-intuitive Ursache-Wirkungs-Beziehung klingt und auf einen
paradoxen Effekt der Arznei hindeutet (und nahezulegen scheint,
dass man selbst bei bohrenden Schmerzen besser nichts nimmt),
wird verständlich, wenn man sich vor Augen führt, dass
Menschen ohne Kopfschmerzen gar nicht zu Mitteln greifen,
während nur die Geplagten lindernde Medizin brauchen (und
sie ihnen normalerweise auch hilft).
Und wenn man erfährt, dass bei sonnigem Winter-Wetter in den
Alpen mehr Ski-Unfälle passieren als bei Nebel, Sturm oder
dichtem Schneetreiben, so bedeutet das keineswegs, dass bessere
Sicht schadet und Unfälle begünstigt. Vielmehr zieht es
bei bestem Sonnenschein sehr viel mehr Skifahrer(innen) auf die
Pisten als bei schlechten Witterungsverhältnissen, weswegen
dann auch mehr Menschen da sind, die verunfallen können. Das
bei schönem Wetter aufkommende Gedränge begünstigt
die Unfälle noch zusätzlich.
Bei überschaubaren Situationen hilft Nachdenken und der
gesunde Menschenverstand. Bei riesigen wahllosen (gar noch
fremden) Datensammlungen und maschineller Suche nach
irgendwelchen Auffälligkeiten und wenn dann vom Computer
eruierte Zufallsbefunde geistlos und ohne zusätzlich
nötigen Test als angeblich 'bewiesen' veröffentlicht
werden, muss man sich über schlechte Ergebnisse nicht
wundern. Sie sind aber nicht fehlerhafter Mathematik, sondern der
unverständigen, falschen Anwendung der richtigen Mathematik
geschuldet.
zum Seitenanfang / zum Seitenende
 Kombinatorik
& Graphentheorie
Kombinatorik
& Graphentheorie
beim Haus vom Nikolaus
(ein Thema, dass nicht 100%-ig zur Stochastik passt, aber noch
weniger zu meinen übrigen Großkapiteln.
Und Baumdiagramme sind in der Kombinatorik ja üblich - vgl.
auch mein Programm WktBaum,
mit Beispiel auf Seite 3 der pdf-Datei stoch_s2.pdf,
siehe oben auf dieser Seite bei 'Stochastik
in der SII')
Selten habe ich mit meiner Intuition so daneben gelegen wie
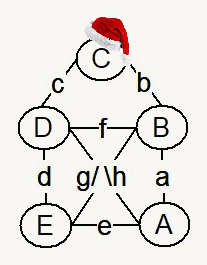
beim schon aus der Kindheit bekannten Haus vom Nikolaus. Am
6.12.2023 las ich auf einem Kalenderblatt, dass es angeblich 44
Lösungen (und wenn man die spiegelbildlichen Lösungen
hinzu nimmt, sogar 88 verschiedene Möglichkeiten) geben
soll, das Haus richtig in einem Zug zu zeichnen. Das würde
bedeuten, dass es 88 (44) unterschiedliche Streckenzüge
geben müsste, die die fünf Punkte ("Knoten") A, B,.., E
entsprechend der Skizze verbinden, wobei in jedem Streckenzug
jede Strecke ("Kante") a, b,.., h genau einmal vorkommt und der
Stift nicht abgesetzt wird. Ich konnte das Haus gerade auf zwei
verschiedene Arten zeichnen und glaubte an einen Fehler der
Kalenderredaktion.
Dabei ist klar, dass die beiden unteren Ecken, nämlich die
Knoten A und E, Anfangs- bzw. Endpunkt sein müssen, weil nur
von diesen beiden Knoten eine ungerade Anzahl von Kanten abgeht
(jeweils 3 -- also Start oder Ende mit einer Kante und ein
zusätzliches Vorbeilaufen am Knoten mit einer ankommenden
und einer abgehenden Kante). An allen anderen Knoten beginnt oder
endet eine gerade Zahl von Kanten (4 bei B und D, 2 bei C), d.h.,
wenn man längs einer Kante zum Knoten kommt, kann/muss man
längs einer anderen Kante den Knoten wieder verlassen. A und
E lagen also außen fest, die übrigen drei Knotenpunkte
B, C, D kann man nur auf 3! = 6 Arten dazwischen anordnen.
Aber halt, es geht ja nicht darum, jeden Knoten genau einmal zu
betreten ("Hamilton-Weg"), sondern jede Kante muss genau einmal
durchlaufen werden ("Euler-Weg". Weil Anfangs- und Endpunkt
verschieden sind, hier kein "Euler-Kreis" wie beim
"Königsberger Brückenproblem" erhofft).
Grundsätzlich können die 8 Buchstaben a, b,.., h in 8!
= 40 320 verschiedenen Reihenfolgen angeordnet werden;
allerdings sind viel weniger Anordnungen (Permutationen ohne
Wiederholung) auch gültige Streckenzüge. So kann
beispielsweise die Kante c nie direkt vor oder nach a durchlaufen
werden (weil a und c keinen gemeinsamen Knoten berühren),
während b immer direkt vor oder direkt nach c im Streckenzug
stehen muss. Die Geometrie der Zeichnung muss beachtet werden,
was ganz viele theoretische Anordnungen ausschließt. Dabei
darf jede Kante in beliebiger Richtung, aber eben nur einmal im
Streckenzug, durchlaufen werden: Das Haus vom Nikolaus ist ein
"bidirektionaler Graph".
Eine weitaus kleinere Obergrenze für die Zahl möglicher
Lösungen erhält man, wenn man die Knoten im Bild
genauer ansieht: Beginnt man in A, so stehen 3 Wege zur
Verfügung (a, e und h). Erreicht man von dort E, so gibt's 2
und nach Erreichen von B oder D noch jeweils 3 Wege (denn der
jeweilige Hinweg darf nicht nochmal betreten werden). Also ist 3
* 2 * 3 * 3 = 54 eine realistische Obergrenze für die Anzahl
der verschiedenen Streckenzüge bzw. Lösungen des
Haus-vom-Nikolaus-Problems. Denn wenn man zu C oder erneut zu B
oder D kommt, bleibt keine Wahlmöglichkeit mehr. Es gibt
jeweils nur noch einen freien Weg, auf dem man den Knoten
verlassen muss.
Nach diesen Überlegungen schienen die 44 Lösungen
(zwischen den mindestes 2 oder 6 und höchstens 54) durchaus
plausibel; eine kurze Internetrecherche bestätigte die
Kalender-Angabe, etwa auf Wikipedia oder bei Alfred Fuchs. Allerdings befriedigten die
fertigen Zeichnungen der 44 Streckenzüge auf den genannten
Webseiten meine Neugier nicht ganz (die anderen 44 Lösungen
erhält man durch Rückwärtsdurchlaufen der
Streckenzüge, s.u.): Nach der anfänglichen
Fehleinschätzung war mein Ehrgeiz geweckt, in einem
Baumdiagramm alle Lösungen und vor allem auch alle
Sackgassen zu finden.
Dabei kann man den Baum insbesondere nach zwei verschiedenen
Strategien zeichnen: Man beginnt mit A als Anfang ("Wurzel") und
verfolgt einen Streckenzug komplett bis zum Ende E, d.h. zeichnet
zunächst nur einen einzigen vollständigen Ast ("Pfad")
des Baums -- etwa nur den Pfad zur Lösung 1 mit allen acht
Kanten. Diese Methode wird in der Graphentheorie und auf meiner
Seite Informatik mit Java, Teil g) Abstrakter Datentyp Graph
als "Tiefensuche" bezeichnet (der Name wird verständlicher,
wenn man den Baum nicht auf der Seite liegen lässt [mit dem
Startknoten A als Wurzel am linken Rand], sondern um 90°
nach rechts [im Uhrzeigersinn] dreht, sodass er kopfüber
hängt und die Wurzel A oben ist. Dann geht der Pfad von der
Wurzel A bis zum Ziel E in die Tiefe). Danach beginnt man wieder
oben und geht zur nächsten Lösung in die Tiefe und baut
so nacheinander Pfad um Pfad den Lösungsbaum auf.
Die andere Strategie besteht darin, an jedem Knoten nicht nur
eine, sondern sofort alle noch betretbaren Kanten zu den direkt
erreichbaren Nachbarknoten zu zeichnen, und so den Baum von der
Wurzel aus Schicht für Schicht aufzubauen (von jedem Knoten
im hängenden Baum also in die Breite zu gehen), wobei man
erst bei nahezu komplettem Baum in der letzten Schicht die erste
und dann praktisch sofort auch alle anderen Lösungen
erhält. Das wäre die so genannte "Breitensuche".
Für beide Strategien habe ich Algorithmen und Java-Programme
(Applications) auf meiner Informatik-Seite g) vorgestellt, die dort allerdings
nicht alle Lösungen produzieren, sondern nach Erreichen
jeweils einer Lösung enden. Insofern müssten die
Programme dort noch etwas angepasst werden.
Aber ich wollte ja nicht ein Programm oder einen KI-Bot mit
dem Erstellen des Baums beauftragen, sondern hoffte, beim
händischen Zeichnen und eigenen Überlegen an jedem
Knoten bzw. an jeder Verzweigung im Baum ein besseres Gefühl
für das anfangs so schlecht eingeschätzte Problem zu
gewinnen. Das gelang tatsächlich, wenngleich das Erstellen
des Baums ein ziemlich langwieriger, viel Fleiß und
Gewissenhaftigkeit erfordernder Prozess war. Ich bin dabei mit
einer Mischung aus Breiten- und Tiefensuche vorgegangen: Nach den
ersten 2..3 Schichten habe ich einzelne Pfade (Streckenzüge)
bis zum Ende verfolgt. Um nichts zu übersehen, habe ich bei
jedem Knoten die noch möglichen, bisher nicht
betretenen/benutzten Kanten in alphabetischer Reihenfolge
abgearbeitet. Außerdem habe ich immer die beiden Kanten b
und c mit dem dazwischenliegenden Knoten C (also das Dach des
Hauses) als eine Einheit, d.h. praktisch wie eine Kante,
behandelt und dadurch nur 7 Schichten gezeichnet. Insgesamt
wunderte mich etwas, dass es nur erstaunlich wenige Sackgassen
gab (zehn, mit S_1 bis S_10 bezeichnet), während die meisten
Versuche problemlos direkt zu Lösungen führten.
Allerdings schöpfen 44 vollständige Lösungen und
10 Sackgassen zusammen genau die oben bestimmte Obergrenze von
höchstens 54 Möglichkeiten aus, sodass auch nicht mehr
Sackgassen zu erwarten waren.
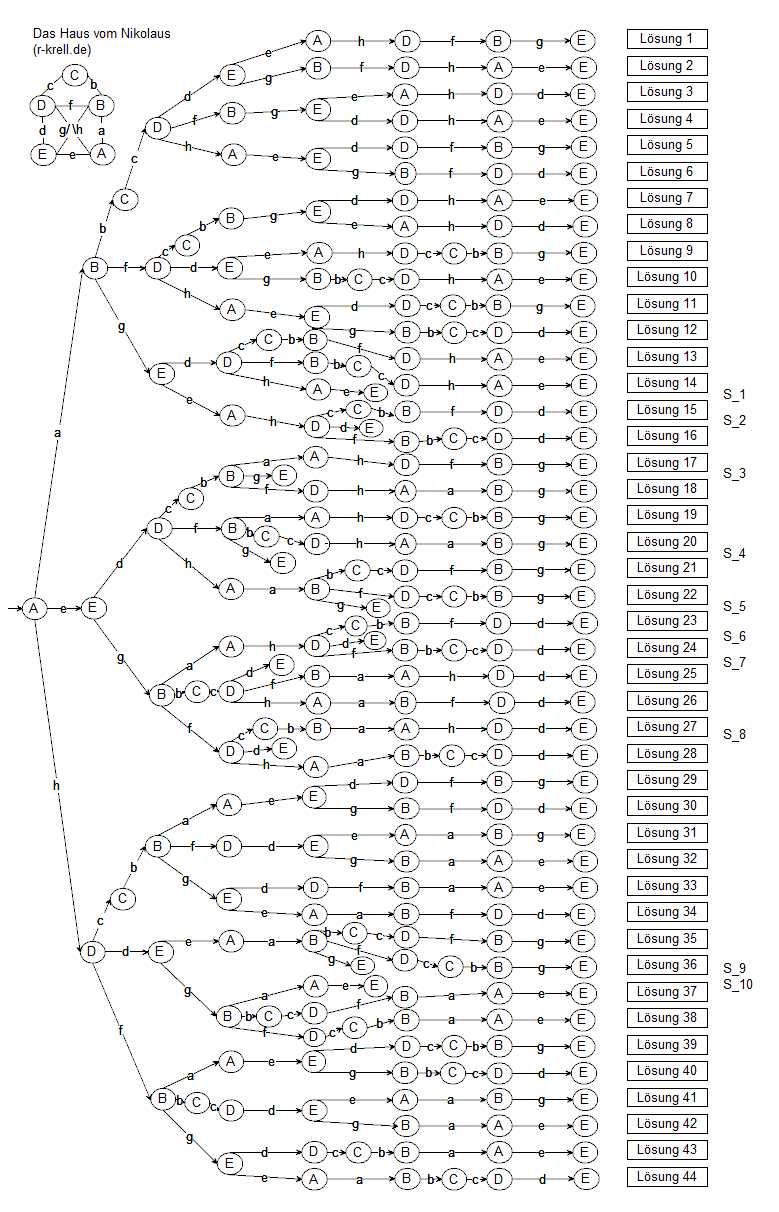
Hier wurden, wie bereits erwähnt, nur die Lösungen
mit dem Anfangspunkt A gezeichnet. Der beispielhaft
herausgegriffen Pfad zur Lösung 7, also , führt zum linken gezeichneten Haus
vom Nikolaus:
, führt zum linken gezeichneten Haus
vom Nikolaus:
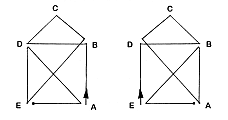
Der gespiegelte Weg rechts beginnt bei E ( ), und ist oben im Baum
zu finden, wenn man den Pfad zur Lösung 23
rückwärts, d.h. von rechts (E) nach links (A) liest
(Bei Alfred Fuchs wäre das übrigens seine
Lösung 26, während Wikipedia diesen Weg als Lösung (38) kennt --
Stand März 2024). Auch die rückwärts gelesenen
Sackgassen führen wieder zu Sackgassen, jetzt mit dem
Anfangspunkt E und vorzeitigem Ende in A. In den Knoten mit einer
geraden Anzahl von zu- oder abführenden Kanten kann keine
Sackgasse enden.
), und ist oben im Baum
zu finden, wenn man den Pfad zur Lösung 23
rückwärts, d.h. von rechts (E) nach links (A) liest
(Bei Alfred Fuchs wäre das übrigens seine
Lösung 26, während Wikipedia diesen Weg als Lösung (38) kennt --
Stand März 2024). Auch die rückwärts gelesenen
Sackgassen führen wieder zu Sackgassen, jetzt mit dem
Anfangspunkt E und vorzeitigem Ende in A. In den Knoten mit einer
geraden Anzahl von zu- oder abführenden Kanten kann keine
Sackgasse enden.
Erstaunlich, welche Herausforderung und Einsichten sich aus
dem einfachen Kinderproblem ergeben haben.
Bei so viel Nikolaus in Weihnachtsstimmung? Oben gibt's noch
Hinweise auf einige mathematische
Adventskalender!
zum Seitenanfang / zum Seitenende
Spielplan
der Fußball-Europameisterschaft 2024
Natürlich ist es auch ein kombinatorisches Problem, den
Spielplan für eine Meisterschaft aufzustellen:
Schließlich sollen in der Vorrunde (Gruppenphase) innerhalb
jeder Gruppe alle Mannschaften einmal gegeneinander spielen. In
der K.O.- bzw. Turnier-Phase müssen zunächst im
Achtelfinale die 16 Qualifikanten aus den Gruppen und später
dann die Sieger aller Spiele aus der jeweils vorangegangenen
Finalrunden gegeneinander antreten. Bei der Fußball-EM 2024
("Euro 2024") in im Sommer 2024 in Deutschland fiel auf, dass bei
den letzten Gruppenspielen manche eigentlich als stark
eingestuften Mannschaften sich mit schlechten Ergebnissen
gegenüber schwachen Gegnern zufrieden gaben und nicht die
erwartete Kampfkraft zeigten Der Fußballer Thomas
Müller befürchtet Absicht, wenn vor dem Spiel bereits
klar ist, welche Fußball-Mannschaften aus einer Gruppe auch
ohne zusätzlichen Sieg weiter kommen werden:
Die
größte Ungerechtigkeit der EM - Unfairer Modus bedarf
der Reform
Kann die Mathematik helfen, einen gerechteren Spielplan zu
erstellen, sodass auch in den letzten Gruppenspielen noch
ernsthaft gekämpft werden muss -- und sich nicht manche
guten Mannschaften für die nächste Phase schonen
können, während sich Mannschaften mit frühen
Spieltagen voll einsetzen mussten?
Resultate nachlesen? Die Ergebnisse der Fußball-EM 2024
finden sich noch auf vielen Seiten im Netz, z.B. auf den
offiziellen UEFA-Seiten getrennt für die Gruppen- sowie die Turnierphase, oder auf einer Seite von der Bild-Zeitung.
zum Seitenanfang / zum Seitenende
Analysis
in Unterricht und Alltag
Außer in den nachfolgenden Abschnitten
findet sich außerdem viel Analysis in der "Mathematik zu Corona" sowie natürlich in
meinen Klausuren!
Einführung
in die Integralrechnung
u.a. mit Fotovoltaik und Weinflasche
Im Leistungskurs 12 (jetzt Q1) hatte ich das
(Riemannn-)Integral bzw. zunächst die Idee der Summenbildung
für die Flächenbestimmung mit Daten unserer damaligen
Fotovoltaik-Anlage eingeführt (vgl. meine "Fotovoltaik"-Hauptseite). Dann wurde in einem
Rollenspiel zwischen Käufern und Verkäufern um die
Größe einer krummlinig berandeten Wiese gefeilscht.
Mit Excel-Arbeitsblättern wurde anschließend die
Wiesenfläche durch Ober- und Untersummen hinreichend genau
bestimmt. Näheres gibt's auf der
Extra-Seite:
Integralrechnung/Flächenberechnung mit Fotovoltaik-Daten,
einer Wiese und Excel
Und weil ich 2005 an einem MuPAD-Kurs teilgenommen hatte, habe
ich die damals im Unterricht "normal" (also ohne das
CAS-Programm) durchgeführte Bestimmung des Volumens einer
Weinflasche zur meiner Übung mit dem Programm dokumentiert.
Das erstellte Notebook wurde im Mai 2005 auf dem MuPAD-Server
veröffentlicht. Nachdem MuPAD seit Oktober 2008 nicht mehr
als eigenständiges Programm existiert, wurden allerdings
auch die MuPAD-Webseiten eingestellt. Vorübergehend war --
bis Sommer 2009 -- auf private Initiative eines
MuPAD-Mitarbeiters ein Großteil des Materials noch auf dem
Bildungsserver der Zentrale für Unterrichtsmedien
erreichbar. Jetzt gibt es offenbar keine zusammenhängende
Sammlung der Materialien mehr. Natürlich können Sie
meinen Beitrag hier in meinem Webangebot ansehen bzw. herunter
laden. Die vielen dort eingearbeiteten Verweise auf andere
MuPAD-Seiten gehen allerdings inzwischen ins Leere...
RotationskoerperWeinflasche.pdf
(190 kB)
Rotationskoerper_Weinflasche.mnb (ca. 400 kB; Notebook
für MuPAD 3.1)
bzw. Rotationskoerper_Weinflasche.mn (ca. 250 kB; für
MuPAD 4)
Hinweise: Die Einführung in die Integralrechnung mit
Fotovoltaik, Excel und der Wiese ebenso wie die Weinflasche
wurden im Mai 2005 auch als MUED-Unterrichtseinheiten (AN-09-04
bzw. AN-10-05) aufgenommen und können von MUED-Mitgliedern
unter http://www.mued.de im SII-Analysis-Bereich als
pdf-Dateien eingesehen bzw. herunter geladen werden.
Außerdem diente mir die Wiese als Testaufgabe bei der
Besprechung der CAS-Programme Derive, MuPAD und GeoGebra auf
meiner Seite "Rezensionen von
Mathematik-Software, Teil c)" (s.o.).
zum Seitenanfang / zum Seitenende
Können
Wirtschaftswissenschaftler und Banker keine
Mathematik?
Beim Besuch einer Filiale der Deutschen Bank fiel mir auf der
Rückseite des ‚Perspektiven'-Hefts 08-09/2018 ein
Artikel ins Auge. Unter der Überschrift ‚Serie
Finanzwissen: Konjunkturzyklus' wurden die klassischen vier
Phasen wirtschaftlicher Entwicklung beschrieben und durch
folgenden Graphen illustriert:
Ich stolperte über die Bezeichnung der markierten Punkte
im Graphen, die in der Mathematik ja als Extrem- und keineswegs
als Wendepunkte bekannt sind. Eine e-Mail-Nachfrage, ob die
Wendepunkte nicht richtigerweise an den Übergängen
zwischen den einzelnen Phasen zu finden wären, ergab, dass
man bei der Redaktion durchaus die Analysis kennt: "Sie haben
natürlich Recht, wenn Sie anmerken, dass in der Mathematik
der Wendepunkt für den Punkt steht, an dem der Graph sein
Krümmungsverhalten ändert. In der Volkswirtschaftslehre
wird der Begriff Wendepunkt im Zusammenhang mit der Darstellung
der Konjunkturphasen - zumal bei vereinfachten Darstellungen -
jedoch so verwendet, wie wir es in ‚Perspektiven' getan
haben...". Zum Beleg wurde auf eine Reihe von
Online-Publikationen mit gleichem Sprachgebrauch verwiesen, u.a.
auf einen Artikel aus dem renommierten Gabler's
Wirtschaftslexikon oder auf eine Veröffentlichung der Bundeszentrale für
politische Bildung, die auf dem Wirtschafts-Duden beruht.
Offenbar geht die abweichende Bezeichnung auf den
Österreicher/Deutschen/US-Amerikaner Joseph Alois Schumpeter
(1883-1950) zurück. Er war eine schillernde
Persönlichkeit, hat wohl erstmals in größerem
Stil mathematische Formeln zur Beschreibung wirtschaftlicher
Vorgänge verwendet und bahnbrechende Theorien über die
wirtschaftliche Entwicklung aufgestellt - die auch heute nach der
Bankenkrise 2008 ff wieder weltweit Beachtung finden. Im
Gegensatz zum gleich alten Briten John Maynard Keynes (1883-1946)
konnte er die Weltwirtschaftskrise um 1930 besser erklären.
Seiner Meinung nach ist aber nicht primär Geldgier, sondern
Kreativität und unternehmerische Innovation der Motor der
Konjunktur: Neues (und oft, aber nicht immer Besseres) führt
zur Verdrängung bzw. ‚Schöpferischen
Zerstörung' des Alten. Wirtschaftliche Umbrüche und
Krisen haben seiner Meinung nach eine nötige
Reinigungswirkung. Der Kapitalismus führe allerdings zu
zunehmender Ungleichverteilung und schaffe sich langfristig
selbst ab. Von Schumpeter sind viele Bonmots überliefert
(u.a.: "Eher legt ein Hund einen Wurstvorrat an, als dass eine
demokratische Regierung Haushaltsrücklagen bildet"). Ob aber
die Umbenennung von Extrem- zu Wendepunkten als bewusster Akt der
schöpferischen Zerstörung überkommener
Mathematik-Traditionen gedacht (oder einfach ein Versehen) war,
ist nicht bekannt. In der Schule - laut Wikipedia legte er das
Abitur bzw. die Matura am Theresianum in Wien ab - soll
Schumpeter jedenfalls sehr gut gewesen sein.
Und ehrlicherweise ist die nun seit fast 90 Jahren übliche
Begriffsverwendung durch die Nationalökonomen fast
naheliegender als der unglückliche mathematische
Sprachgebrauch von "Wendepunkt". Denn die Verwendung des Begriffs
in der Mathematik hat ja mit Wenden (im alltäglichen Sinne
von Umkehren) wenig zu tun und weckt eher irreführende
Assoziationen - wie jede Mathe-Lehrerin und jeder Mathe-Lehrer
weiß, der den Begriff jedes Jahr unvoreingenommenen
Schülerinnen und Schülern der Einführungsphase
nahebringen muss. "Krümmungswechselpunkt" wäre sicher
die bessere, verständlichere mathematische Bezeichnung.
Bleibt noch die Frage, ob die Konjunkturfunktion als
eigenständige Funktion eher uninteressant ist, aber als
Ableitungsfunktion zur Beschreibung der zeitlichen Änderung
einer wichtigeren Größe mehr Sinn macht. Denn die
Extremstellen der Konjunkturfunktion wären die
(mathematischen) Wendestellen ihrer Stammfunktionen. Allerdings
hat das Integral ‚Konjunktur mal Zeit' offenbar keine
wirtschaftlich sinnvolle Bedeutung, der Konjunkturverlauf selbst
hingegen schon, sodass hier kein Grund für die
Begriffsveränderung gefunden wird.
zum Seitenanfang / zum Seitenende
Entspricht ein
Hundejahr sieben Menschenjahren?
 Anfang Juli 2020 konnte man
vielerorts lesen (online u.a. bei n-tv oder web.de), dass die altbekannte Faust- bzw.
Pfoten-Regel "1 Hundejahr = 7 Menschenjahre" ausgedient
habe. Zweifel waren bisher schon angebracht, weil Hunde meist
schon nach einem Dreivierteljahr geschlechtsreif werden -- was
nur 5,25 Menschenjahren entspricht. Kalifornische Biologen haben
nun durch Vergleich der Methylierung der Erbsubstanz in den
Zellen festgestellt, dass dieser Alterungsprozess bei Hunden und
bei Menschen unterschiedlich schnell abläuft und nicht
linear (d.h. direkt proportional) korreliert ist. Die Zell-DNA
der etwas über 100 untersuchten Labrador-Hunde
verändert sich anfangs viel schneller und später
relativ langsamer als beim Menschen. Angeblich würde der
Zusammenhang durch die neue Formel
Anfang Juli 2020 konnte man
vielerorts lesen (online u.a. bei n-tv oder web.de), dass die altbekannte Faust- bzw.
Pfoten-Regel "1 Hundejahr = 7 Menschenjahre" ausgedient
habe. Zweifel waren bisher schon angebracht, weil Hunde meist
schon nach einem Dreivierteljahr geschlechtsreif werden -- was
nur 5,25 Menschenjahren entspricht. Kalifornische Biologen haben
nun durch Vergleich der Methylierung der Erbsubstanz in den
Zellen festgestellt, dass dieser Alterungsprozess bei Hunden und
bei Menschen unterschiedlich schnell abläuft und nicht
linear (d.h. direkt proportional) korreliert ist. Die Zell-DNA
der etwas über 100 untersuchten Labrador-Hunde
verändert sich anfangs viel schneller und später
relativ langsamer als beim Menschen. Angeblich würde der
Zusammenhang durch die neue Formel
vergleichbare Menschenjahre = 16 *
ln (Hundejahre) + 31
viel zutreffender ausgedrückt. Dabei ist ln der
natürliche Logarithmus, d.h. der Logarithmus zur Basis
e (e = Eulerzahl, ungefähr 2,718..).
Spätestens wenn man den Graph zeichnet, erscheint die Formel
für junge Hunde allerdings wenig plausibel:
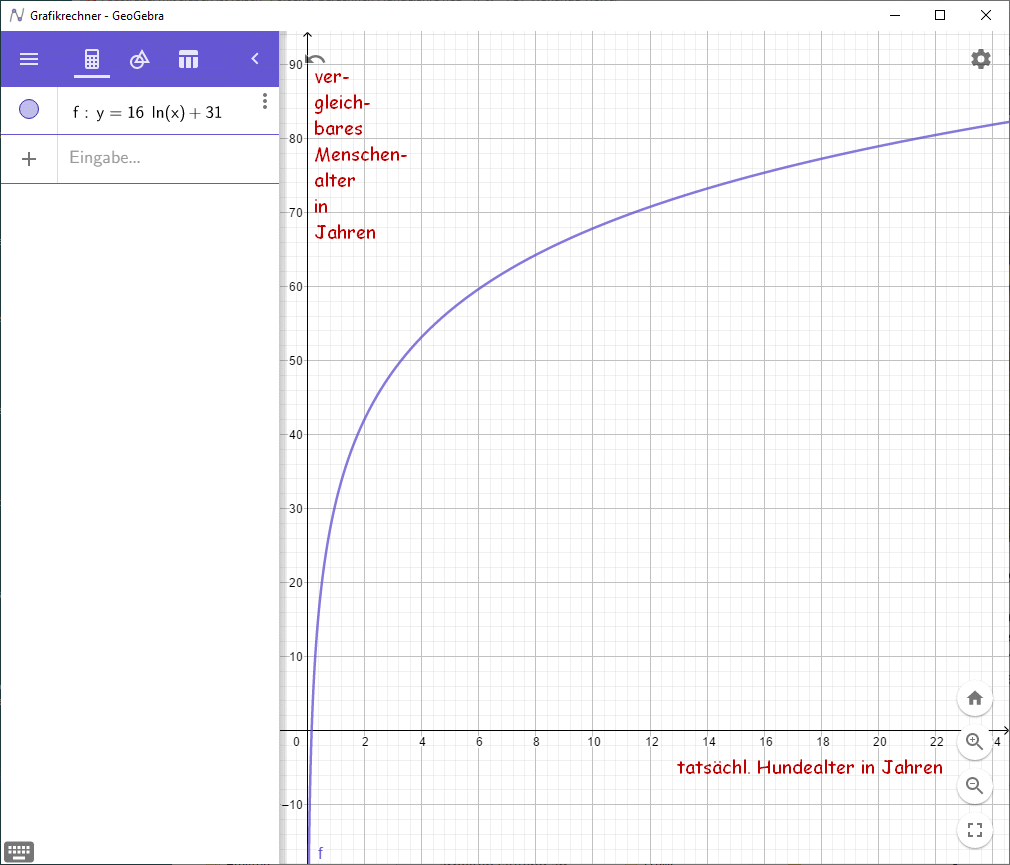
Denn danach würden Hunde nicht mit null geboren, sondern
mit einem beliebig negativen Menschenalter starten! Denn der
ln ist für 0 gar nicht definiert und hat für
kleine positive Argumente stark negative Werte, d.h. geht bei
'Hundejahre gegen null' gegen Minus-Unendlich. Erst bei einem
Hundealter von etwa 52 Tagen wird das vergleichbare Menschenalter
erstmals positiv. Die Arbeitsgruppe von Wang, Ma, Hogan,... u.a.
am Lehrstuhl von T. Ideker an der Universität von San Diego
zeigt in der Online-Veröffentlichung (die Ende August
2020 offenbar unverändert gedruckt wurde) den gleichen
Graphen (Bild 3D auf der mit "4" nummerierten fünften Seite
der pdf-Datei), ignoriert aber das Problem, obwohl auch dort der
Graph erkennbar nicht durch den Ursprung geht. Es werden dort
weder konkrete Wertepaare genannt -- sondern nur eine Fläche
gefärbt (Bild 3A) bzw. Punktwolken für nur fünf
(am besten passende?) Hunde gezeichnet (Bilder 3B und 3C). Es
wird auch nie erwähnt, warum überhaupt eine
logarithmische Regression gewählt wurde. Man erfährt
lediglich, dass die Formel eine Art Kompromiss zwischen
"Menschenjahre = 17 * ln (Hundejahre)+33" und
"Menschenjahre = 16 * ln (Hundejahre)+30" sein soll.
Diese beiden Formeln weisen schon das gleiche Problem mit der
Null auf und wurden ebenfalls nie begründet.
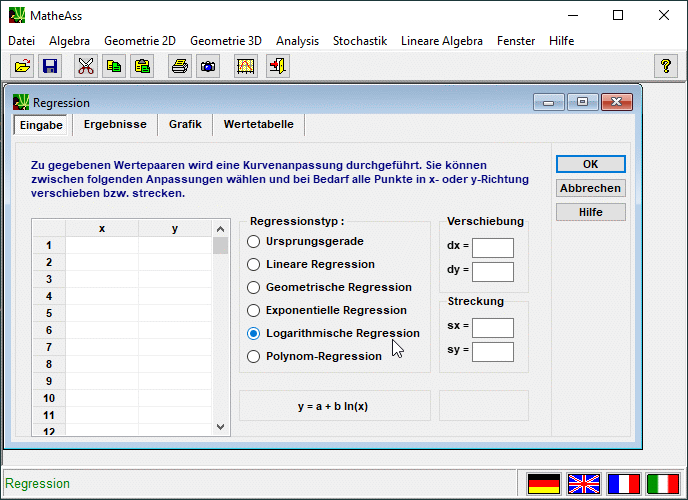 Wahrscheinlich wurde zur Ermittlung der Formeln ein
Mathematik-Programm wie z.B. MatheAss
(abgebildet ist hier noch die Version 8.1) benutzt, das
verschiedene Regressionen anbietet. Weil die Graphen der meisten
anderen Funktionstypen nicht oder in die falsche Richtung
gekrümmt wären und daher viel ungeeigneter waren, blieb
offenbar die logarithmische Variante übrig. Und weil dann
der grobe Verlauf ab dem 2. (Hunde-) Monat in etwa passte, haben
sich die Biologinnen und Biologen anscheinend keine weiteren
Gedanken zur Gültigkeit der Formel oder zu mathematischen
Implikationen gemacht und keine (vermutlich auch in ihrem
Programm mögliche und nötige) geringfügige
Verschiebung probiert, mit der das Problem hätte verborgen
werden können, wenn z.B. "Menschenjahre = 16 * ln
(Hundejahre + 0,144) + 31" gefunden worden wäre. Allerdings
ist nicht einsichtig, wieso überhaupt ein logarithmischer
Zusammenhang bestehen soll. Denn anders als in der Physiologie,
wo die subjektive Reizwahrnehmung ungefähr logarithmisch mit
der objektiven Reizintensität zunimmt (was zum
Weber/Fechner-Gesetz führte), gibt es hier keinerlei
Kausalkette. Es wäre besser gewesen, die Zusammenhänge
in einer empirischen Tafel (ähnlich den Diagrammen von
Babynahrungsherstellern für typische Größen und
Gewichte von Säuglingen) mit breitem Streubereich
darzustellen. Wenn zur Bequemlichkeit doch eine Formel gefunden
werden soll, hätte meiner Meinung nach eher eine liegende
Parabel ausprobiert werden sollen, also eine Potenzfunktion der
Form "Menschenalter = A * Hundelalter B ",
wobei der Exponent B zwischen 0 und 1 liegen müsste (in
MatheAss als 'Geometrische Regression' zu finden). Solche
Funktionen gehen immer durch den Ursprung (weswegen MatheAss
ärgerlicherweise den redundanten Messpunkt (0|0) als
unzulässig zurückweist). Aber ohne die Messwerte der
Hundestudie können weder A noch B berechnet werden, noch
kann beurteilt werden, ob nicht ein mal links-, mal
rechtsgekrümmter Spline besser passen würde.
Schade.
Wahrscheinlich wurde zur Ermittlung der Formeln ein
Mathematik-Programm wie z.B. MatheAss
(abgebildet ist hier noch die Version 8.1) benutzt, das
verschiedene Regressionen anbietet. Weil die Graphen der meisten
anderen Funktionstypen nicht oder in die falsche Richtung
gekrümmt wären und daher viel ungeeigneter waren, blieb
offenbar die logarithmische Variante übrig. Und weil dann
der grobe Verlauf ab dem 2. (Hunde-) Monat in etwa passte, haben
sich die Biologinnen und Biologen anscheinend keine weiteren
Gedanken zur Gültigkeit der Formel oder zu mathematischen
Implikationen gemacht und keine (vermutlich auch in ihrem
Programm mögliche und nötige) geringfügige
Verschiebung probiert, mit der das Problem hätte verborgen
werden können, wenn z.B. "Menschenjahre = 16 * ln
(Hundejahre + 0,144) + 31" gefunden worden wäre. Allerdings
ist nicht einsichtig, wieso überhaupt ein logarithmischer
Zusammenhang bestehen soll. Denn anders als in der Physiologie,
wo die subjektive Reizwahrnehmung ungefähr logarithmisch mit
der objektiven Reizintensität zunimmt (was zum
Weber/Fechner-Gesetz führte), gibt es hier keinerlei
Kausalkette. Es wäre besser gewesen, die Zusammenhänge
in einer empirischen Tafel (ähnlich den Diagrammen von
Babynahrungsherstellern für typische Größen und
Gewichte von Säuglingen) mit breitem Streubereich
darzustellen. Wenn zur Bequemlichkeit doch eine Formel gefunden
werden soll, hätte meiner Meinung nach eher eine liegende
Parabel ausprobiert werden sollen, also eine Potenzfunktion der
Form "Menschenalter = A * Hundelalter B ",
wobei der Exponent B zwischen 0 und 1 liegen müsste (in
MatheAss als 'Geometrische Regression' zu finden). Solche
Funktionen gehen immer durch den Ursprung (weswegen MatheAss
ärgerlicherweise den redundanten Messpunkt (0|0) als
unzulässig zurückweist). Aber ohne die Messwerte der
Hundestudie können weder A noch B berechnet werden, noch
kann beurteilt werden, ob nicht ein mal links-, mal
rechtsgekrümmter Spline besser passen würde.
Schade.
Die von Wang u.a. genannte Formel kann jedenfalls nicht ohne
Weiteres akzeptiert werden. Möglicherweise haben sich die
Forscher bei der für sie vielleicht eher fremden Mathematik
unhinterfragt auf die scheinbare Autorität eines Programms
verlassen, auch wenn sie die Software eventuell nicht
vollständig bedienen wollten oder konnten bzw. das
übernommene Ergebnis nicht geprüft oder verstanden
haben. Ähnliches findet man leider immer wieder selbst bei
Wissenschaftlern, die in ihrem eigentlichen Fachgebiet durchaus
hervorragende Leistungen erbringen. Jedenfalls können
Skepsis und Plausibilitätsprüfungen nie schaden, bevor
man sich auf gefundene Formeln verlässt. Von Medien, die
über die Studie berichten, ist jedenfalls keine eigene
Kontrolle zu erwarten -- weder von den beiden eingangs genannten
deutschen Quellen, noch von den auf die Ankündigung
wissenschaftlicher Neuerscheinungen spezialisierten Fachportalen,
wie etwa der englischsprachigen Webseite genengnews. Hoffentlich sind die
Zelluntersuchungen verständiger durchgeführt worden und
die herangezogene DNA-Metylierung kann als verlässlicher
Indikator für den gesamten Alterungsprozess gelten. Auf
meine eMail mit den Bedenken zu seiner Formel hat Herr Wang
leider nicht reagiert.
P.S.: Seit der Version 9.0 von MatheAss
beherrscht das (für Privatanwender jetzt kostenfreie)
Mathematik-Programm als weiteren Regressionstyp die "logistischen
Regression". Damit kann man jetzt auch Ähnliches wie den
dunkelgrünen Graph auf meiner Corona-Seite bei den
4 Wachstumsmodellen als Ausgleichkurve durch
Wertepaare ermitteln lassen.
zum Seitenanfang / zum Seitenende
Zahlentheorie
Viel Zahlentheorie und Primzahl-Anwendungen
stecken übrigens in modernen kryptografischen Verfahren, die
auf meiner Informatikseite k): "Kryptologie II" ausführlich
dargestellt sind!
Größte
bekannte Primzahl
 Nach
nahezu sechs Jahren hartnäckiger Suche gibt es seit Oktober
2024 einen neuen Rekordhalter: Die zweiundfünfzigste
Mersenne-Primzahl
2 136 279 841 - 1 ist mit
über 41 Millionen Dezimalstellen die größte
bisher bekannte Primzahl. Sie wurde vom Hobbymathematiker Luke
Durant aus Kalifornien entdeckt - allerdings nicht mit einem oder
mehreren gewöhnlichen PCs (wie alle früheren
Riesenprimzahlen), sondern durch den Cloud-koordinierten Einsatz
ganz vieler Grafikkarten unter Beteiligung von über 24
Rechenzentren (vgl. mersenne.org). Die nun nur noch zweitgrößte
bekannte Primzahl ist die von Patrick Laroche aus Florida im
Dezember.2018 entdeckte einundfünfzigste Mersenne-Primzahl
2 82 589 933 - 1. Sie hat nur
knapp 25 Millionen Stellen (die ausgedruckt über 1000 km
lang wären).und wurde 11 Monate nach der im Januar 2018
gefundenen fünfzigsten Mersenne-Primzahl bekannt. Mit der
45. Primzahl war 2008 erstmals die 10-Mio-Dezimalstellen-Grenze
überschritten worden und damit der von der Electronic
Frontier Foundation zum Jahr 2000 ausgelobte Preis von 100 000
US-$ gewonnen worden (den die Organisatoren des GIMPS-Projekts
2009 allerdings unter mehreren Teilnehmern aufgeteilt haben - es
ist ja eher Zufall, wer welche Zahl zum Prüfen kriegt;
s.u.).
Nach
nahezu sechs Jahren hartnäckiger Suche gibt es seit Oktober
2024 einen neuen Rekordhalter: Die zweiundfünfzigste
Mersenne-Primzahl
2 136 279 841 - 1 ist mit
über 41 Millionen Dezimalstellen die größte
bisher bekannte Primzahl. Sie wurde vom Hobbymathematiker Luke
Durant aus Kalifornien entdeckt - allerdings nicht mit einem oder
mehreren gewöhnlichen PCs (wie alle früheren
Riesenprimzahlen), sondern durch den Cloud-koordinierten Einsatz
ganz vieler Grafikkarten unter Beteiligung von über 24
Rechenzentren (vgl. mersenne.org). Die nun nur noch zweitgrößte
bekannte Primzahl ist die von Patrick Laroche aus Florida im
Dezember.2018 entdeckte einundfünfzigste Mersenne-Primzahl
2 82 589 933 - 1. Sie hat nur
knapp 25 Millionen Stellen (die ausgedruckt über 1000 km
lang wären).und wurde 11 Monate nach der im Januar 2018
gefundenen fünfzigsten Mersenne-Primzahl bekannt. Mit der
45. Primzahl war 2008 erstmals die 10-Mio-Dezimalstellen-Grenze
überschritten worden und damit der von der Electronic
Frontier Foundation zum Jahr 2000 ausgelobte Preis von 100 000
US-$ gewonnen worden (den die Organisatoren des GIMPS-Projekts
2009 allerdings unter mehreren Teilnehmern aufgeteilt haben - es
ist ja eher Zufall, wer welche Zahl zum Prüfen kriegt;
s.u.).
Diese preisgekrönte 45. Mersenne-Primzahl wurde 2008
übrigens in Langenfeld im Rheinland (zwischen Köln und
Düsseldorf) entdeckt. Diese inzwischen nur noch
siebtgrößte bekannte Primzahl kann als
2 37 156 667 - 1 angegeben
werden und hat, rechnet man die Potenz (und Differenz) wirklich
aus, 11 182 272 Dezimalstellen!
Die im September 2006 entdeckte 44. Mersenne-Primzahl
232.582.657
- 1 hat nur 9,8 Millionen Stellen und war -- wie schon die 43.
Mersenne-Primzahl -- vom Team unter Curtis Cooper an der Central
Missouri State University gefunden worden (wo dann 2016 auch die
49. Mersenne-Zahl gefunden wurde). Dort werden mehr als 700
Uni-PCs nach Feierabend genutzt. Alle hier genannten Primzahlen
wurden nämlich im Rahmen des GIMPS-Projektes dadurch
erkannt, dass viele PC-Besitzer(innen) ihre(n) Computer zu Hause
(oder in der Uni bzw. am Arbeitsplatz), wenn sie ihn/sie nicht
selber brauchen, in den Dienst der Primzahlprüfung stellen.
So wurde z.B. die 42. Mersenne-Primzahl im Sommer 2005
zufällig nach nur 5 Tagen Rechenarbeit von den 24 Rechnern
in einem deutschen Augenzentrum aufgespürt. Davor hatte ein
kanadischer Schüler nach 45 Tagen Rechenzeit auf seinem
Home-Computer vorübergehend den Rekord mit der bis dahin
größten bekannten Primzahl inne.
Tatsächlich dauert der Test, ob eine um eins verminderte
Zweierpotenz mit großer Wahrscheinlichkeit eine Primzahl
ist, bei heute üblicher Hardware meist nur noch einige Tage
bis einige Wochen. Ist auf Rechnern mit unterschiedlicher
Hardware und mit zwei verschiedenen Programmen eine Zahl als
vermutliche Primzahl erkannt, wird sie bekannt gegeben. Der
endgültige, exakte Test dauert dann aber noch mehrere Jahre.
So konnte erst im Oktober 2021 die 48. Mersenne-Primzahl
endgültig als sicher bestätigt werden; die neueren
Zahlen sind noch nicht völlig sichere Primzahlen.
Selbst wenn man jetzt weiß bzw. mit hoher
Wahrscheinlichkeit annimmt, dass
2 136 279 841 - 1 eine
Primzahl ist, kann man eine solche Zahl nicht mehr auf dem
Taschenrechner anzeigen lassen - auch nicht in wissenschaftlicher
Darstellung (Der Taschenrechner zeigt die ersten zehn oder
zwölf Stellen von maximal 100-stelligen Zahlen an;
längere Zahlen führen zum "Error"). Aber auf dem PC
gelingt es in einigen Tagen bis Wochen, alle einundvierzig
Millionen Stellen aus der gegebenen Potenz zu berechnen. Bisher
konnte jeder selbst dazu das kleine kostenlose WinCalc von Rick
Parris benutzen. Leider ist seit März 2020 WinCalc bzw. das
gesamte Peanut-Mathe-Softwarepaket nicht mehr auf den Seiten der
Philips Exeter Academy in New Hampshire/USA zu finden, wo R.
Parris früher unterrichtet hat. Einzelne Programme findet
man gelegentlich auf Shareware-/Freeware-Seiten; Alternativen
für das gesamte Peanut-Paket nenne ich unten auf dieser
Seite bei den Verweisen (s.u., vorletzter
Link; dort auch zusätzliche Oberfläche).
Im 17. Jahrhundert war dem Mönch und Mathematiker
Mersenne aufgefallen, dass einige Primzahlen eine Darstellung der
Form 2 n - 1 haben, z.B. 3 =
2 2 - 1 oder 7 =
2 3 - 1. Allerdings können
keineswegs alle Primzahlen nach dieser Formel berechnet werden:
5, 11 oder 13 sind zum Beispiel Primzahlen, ohne
Mersenne-Primzahlen zu sein. Andererseits sind viele
Zweierpotenzen minus eins auch keine Primzahlen, wie etwa
2 4 - 1 = 15 = 3 • 5.
Tatsächlich sind im Bereich der größeren Zahlen
die Mersenne-Zahlen sogar sehr selten. Deshalb muss viel probiert
werden - eben auf vielen Computeren im GIMPS-Projekt - bis wieder
eine Mersenne-Zahl entdeckt wird. Und auch unterhalb der jetzt
bekannten größten Primzahl gibt noch ganz viele
unbekannte Primzahlen, die eben nicht als Mersenne-Zahlen
darstellbar sind und noch auf ihre Entdeckung warten! [Mehr
über Mersenne-Primzahlen gibt's z.B. auf den Seiten http://www.achimpassauer.privat.t-online.de/homepage.htm
oder auch bei Wikipedia: http://de.wikipedia.org/wiki/Mersenne-Primzahl].
Beim GIMPS-Projekt (Great Internet Mersenne Prime Search,
inzwischen auf www.mersenne.org) probiert man einfach nacheinander
für alle natürlichen Zahlen n aus, welche
Ergebnisse nach der Formel 2 n - 1
tatsächlich Primzahlen sind. Die allermeisten sind keine
Primzahlen, aber die Zahlen, die zufällig der kanadische
Schüler, der deutsche Augenarzt, das Central-Missouri-Team,
der Langenfelder H. Elvenich, zuletzt Jonathan Pace, Patrick
Laroche oder jetzt Luke Durant überprüft haben, waren
Primzahlen. Viele, viele andere Teilnehmer am GIMPS-Projekt
hatten hingegen Pech: die von ihnen überprüften Zahlen
erwiesen sich nach langem Rechnen doch als teilbar. Dank eines
verbesserten Algorithmus geht die Überprüfung speziell
von Mersenne-Primzahlen inzwischen übrigens rascher!
 Neben
dem altbekannten, oben benutzten Mersenne-Term
2 n - 1 gibt es noch weitere Formeln,
um Kandidaten für einige andere Primzahlen zu finden: So
gilt ebenfalls seit Oktober 2024 als recht sicher, dass sogar
unendliche viele Primzahlen die Gestalt
a 2 + 4 • b 2
haben, wenn schon a und b Primzahlen sind. Das wollen zumindest
Ben Green und Mehtaab Sawhney bewiesen haben. Schon 1997 hatten
John Friedlander und Hendryk Iwaniec gezeigt, dass man auch mit
der Summe a 2 + b 4
unendlich viele Primzahlen produzieren kann. In beiden
Fällen führen längst nicht alle Einsetzungen von
Primzahlen a und b wieder zu neuen Primzahlen -- aber eben doch
unendlich viele! Allerdings scheint es bisher keine schnellen
Prüfverfahren für diese Arten von Primzahlen zu geben,
und Jahrhunderte oder Jahrtausende wollen freiwillige
Primzahlprüfer nicht für jeden Kandidaten
rechnen...
Neben
dem altbekannten, oben benutzten Mersenne-Term
2 n - 1 gibt es noch weitere Formeln,
um Kandidaten für einige andere Primzahlen zu finden: So
gilt ebenfalls seit Oktober 2024 als recht sicher, dass sogar
unendliche viele Primzahlen die Gestalt
a 2 + 4 • b 2
haben, wenn schon a und b Primzahlen sind. Das wollen zumindest
Ben Green und Mehtaab Sawhney bewiesen haben. Schon 1997 hatten
John Friedlander und Hendryk Iwaniec gezeigt, dass man auch mit
der Summe a 2 + b 4
unendlich viele Primzahlen produzieren kann. In beiden
Fällen führen längst nicht alle Einsetzungen von
Primzahlen a und b wieder zu neuen Primzahlen -- aber eben doch
unendlich viele! Allerdings scheint es bisher keine schnellen
Prüfverfahren für diese Arten von Primzahlen zu geben,
und Jahrhunderte oder Jahrtausende wollen freiwillige
Primzahlprüfer nicht für jeden Kandidaten
rechnen...
Einen wirklich praktischen Nutzen haben Primzahlen mit zig
Millionen Stellen allerdings (noch?) nicht: für die
Kryptologie sind sie zu groß (die dort verwendeten
'großen' Primzahlen haben 20 bis maximal 200 Dezimalstellen
und sind besser keine der ja relativ leicht auffindbaren
Mersenne-Zahlen). Die GIMPS-Rechnungen dienen also eher dem
Spaß, der Freude bei der Teilnahme/Teilhabe an etwas
Großem, der Rekordjagd, der Suche nach und dem Test von
immer schnelleren Primzahl-Erkennungs-Programmen und letztlich
auch dem Hardware-Stress: 2016 hat u.a. eine deutsche Gruppe
während ihrer Berechnungen wieder einen Fehler im Prozessor
gefunden. Und vielleicht lockt auch das Geld. Zwar wurde der
Preis aus ihrem Millenium-Aufruf schon 2009 für die 45.
Mersenne-Zahl gezahlt, aber für die erste Primzahl mit
mindestens 100 Millionen Stellen (statt jetzt 41 Millionen) will
die Electronic Frontier Foundation nochmal 150 000 US-Dollar
ausgeben.
Einen Überblick über weitere Projekte geballten
Home-Computereinsatzes im Internet gibt z.B.
http://www.rechenkraft.de
;
spektakulär ist auch die im September 2019 erreichte
Lösung zur Antwort 42 mit rund 500 000 Computern
(s.u.).
Übrigens: Bei dem wohl bekanntesten Projekt mit
verteilter Rechenleistung haben 20 Jahre lang zeitweilig
über drei Millionen PCs in aller Welt daran gearbeitet,
jeweils kleine Stücke der von Radioteleskopen aus dem
Weltraum aufgenommenen Daten nach intelligent wirkenden Mustern
zu durchforsten, um so nach Signalen außerirdischer
Lebewesen zu suchen: Das (inzwischen ausgesetzte bzw. "im
Winterschlaf" befindliche) Seti@home-Projekt hatte damit zeitweise mehr als die
doppelte Rechenkapazität des damals leistungsfähigsten
und schnellsten Supercomputers der Welt, "BlueGene/L", wie die
Physikalisch-Technische Bundesanstalt in ihrer Zeitschrift
"Maßstäbe" im Heft 6 vom September/Oktober 2005 auf der
Seite mit der Nummer 46 (=Seite 48 des pdf-Dokuments) gemeldet
hatte. Im März 2020 werden allerdings die letzten Schnipsel
der empfangenen Daten an die zuletzt noch 1,8 Millionen
Teilnehmer verschickt, wie heise.de meldet. Gefunden wurden in den 20
Jahren trotz aller Mühen aber keinerlei Anzeichen
dafür, dass es Aliens gibt oder sie mit uns in Kontakt
treten wollen. Aber nicht das Ausbleiben fremder Signale
führte zum Ende des Projekts: neue Detektoren in den
Radioteleskopen liefern inzwischen offenbar so schnell und so
viele Daten, dass sie vor Ort vorsortiert und vorgeprüft
werden müssen und belangloses Material direkt verworfen
wird, statt gespeichert und versendet werden kann.
Inzwischen haben aber viele Firmen die Möglichkeiten des
verteilten Rechnens entdeckt; angeblich nutzen vor allem
Pharmaunternehmen ihre Bürocomputer auch schon zur
rechenintensiven Simulation von Molekülstrukturen. Und das
europäische (Kern-)Forschungszentrum CERN, das schon mit der
Erfindung der Hyperlinks und der Entwicklung des WWW (world wide
web) 1993 dem Internet zum Durchbruch verholfen hat, nimmt sich
inzwischen des verteilten Rechnens im Internet an und versucht,
allgemeine Regeln und Verfahren für das Grid-Computing zu
entwickeln, u.a. um die hohe für die Teilchenphysik
benötigte Rechenleistung auf viele Geräte zu verteilen.
Grundsätzliche Informationen gibt's beim Worldwide LHC Computing Grid des CERN oderauf
der BOINC-Übersichtsseite (BOINC = Berkeley Open
Infrastructure for Network Computing im Auftrag von Science
United. Den BOINC-Software-Client kann übrigens auch von
der Seite der Computerzeitschrift Chip herunter geladen werden, damit man die
ungenutzte Rechenleistung seines PC für gerade aktuelle
wissenschaftliche Projekte zur Verfügung stellen kann.
Und verteilte Rechenkraft konnte auch genutzt werden, um die
Entwicklung von Medikamenten und Impfstoffen - wie zuletzt z.B.
gegen das Coronavirus - zu beschleunigen, wie zuerst Jörg Schieb
berichtet: Insbesondere Computer-Spieler waren aufgerufen, ihre
leistungsfähigen Rechner dem Projekt folding@home zur
Verfügung zu stellen, das sich schon vor Covid und jetzt
auch weiterhin der Analyse aktueller Krankheitserreger bzw. dem
"virtuellen Ausprobieren" von neuen Impfstoffen verschrieben
hat.
zum Seitenanfang / zum Seitenende
Schnelle
Primzahlprüfung
Den Informatikern Agarwal, Kayal und Saxena war Ende 2002 in
Indien ein Durchbruch in der Primzahl-Prüfung gelungen.
Um festzustellen, ob eine Zahl Primzahl ist oder nicht, musste
früher mit allen kleineren Zahlen ausprobiert werden, ob sie
die vermutete Primzahl teilen. Zwar konnten einige Zahlen weg
gelassen werden: Will man wissen, ob z.B. 1001 eine Primzahl ist,
ist der größte Teiler, den man probieren muss, die
Wurzel aus 1001 bzw. die nächstkleinere ganze Zahl (hier 31)
(weil Wurzel(p) mal Wurzel(p) die Primzahl p ergibt. Ein
größerer Faktor auf der einen Seite hätte einen
kleineren Faktor auf der anderen Seite zur Folge, so dass die
Kombination schon beim kleinen Faktor gefunden würde). Mit
anderen Worten, man müsste die Divisionen 1001 : 2, 1001 :
3, 1001 : 4, 1001 : 5, .. , 1001 : 31 durchführen und
jedesmal prüfen, ob sie restlos aufgehen. Nur wenn keine
Division mit ganzem Ergebnis gelingt, ist die 1001 eine Primzahl.
Zwar können noch einige mögliche Teiler weg gelassen
werden (wenn 1001 nicht durch 2 teilbar ist, braucht man 4, 6,
8.. oder andere Teiler aus der Zweierreihe nicht mehr probieren -
Gleiches gilt natürlich für alle anderen Reihen!
Außerdem können gerade Zahlen > 2 nie prim sein,
sodass man sich die Überprüfung mit 2 und ihren
Vielfachen sowieso schenken kann). Dies fiel schon vor rund 2300
Jahren dem Griechen Eratosthenes auf ("Sieb des Eratosthenes").
Bleiben auf diese Weise nur 10 % der kleineren Zahlen als
mögliche Teiler übrig, so müssen hier nur 3
Divisionen durchgeführt werden, um festzustellen, ob 1001
prim ist (es sei denn, man hat schon vorher einen echten Teiler
gefunden und weiß deshalb, dass 1001 keine Primzahl
ist).
3 Rechenoperationen gehen bei einem Computer natürlich
blitzschnell. Um herauszufinden, ob die etwa zehn Mal so
große Zahl 10 001 eine Primzahl ist, wären dann 10%
von Wurzel(10 001), also etwa 10 Operationen nötig. Für
jede zusätzliche Stelle der Primzahl verdreifacht sich
ungefähr die Anzahl der Divisionen. Um die neun- bzw.
zehnstellige Zahl 1 000 000 001 = 10 9 + 1 auf ihre
Primzahleigenschaft zu prüfen, wären dann 31 621
Divisionen nötig - mit einem Computer in wenigen Sekunden
machbar.
Und für eine vermutete Primzahl mit 4 Millionen
Dezimalstellen wären nach diesem Verfahren nicht etwa 400
000 (= 10 % von 4 Millionen) Divisionen, sondern 0,1 • 10
2 000 000 (= 10 % von Wurzel(10
4 000 000)) Divisionen nötig. Selbst
ein schneller Computer, der pro Sekunde 10 000 Divisionen
durchführen kann, wäre damit 0,1 • 10
2 000 000 Sekunden = 2,7 • 10
1 999 995 Stunden = 3,2 • 10
1 999 991 Jahre beschäftigt. Ziemlich
lange, wenn man bedenkt, dass unser Weltall bisher nur etwa 13,7
Milliarden Jahre = 1,37 • 10 10 Jahre alt ist.
Auch die Vertausendfachung der Rechenleistung bringt hier keinen
spürbaren Gewinn (dann wären es "nur" noch 3,2 •
10 1 999 989 Jahre!). Außerdem ist hat
die inzwischen größte Primzahl nicht 4, sondern fast
25 Millionen Stellen.
Jedes Rechenverfahren, dessen Aufwand mit dem Wert der
untersuchten (Prim-)Zahl ansteigt (das also mit dem Exponenten
oben an der 10 wächst, weswegen man von exponentiellem
Aufwand spricht), ist für große Zahlen nicht mehr in
annehmbarer Zeit durchführbar. Für eine Reihe von
Problemen (u.a. der Suche nach einem optimalen Stundenplan) sind
bisher nur Verfahren mit exponentiellem Aufwand bekannt (weswegen
sich praktische Verfahren mit einem nicht optimalen Stundenplan
begnügen müssen). Auch das verbreitete
RSA-Verschlüsselungsverfahren macht sich zu Nutze, dass eine
Entschlüsselung nach der durchaus bekannten Methode
wahrscheinlich so viele Jahre bzw. Jahrzehnte dauern würde,
dass bis dahin jede Nachricht ihren Wert verloren hat.
Erst seit etwa 1985 gibt es schnellere Verfahren für die
Prüfung auf die Primzahl-Eigenschaft, die aber zum Teil
stochastische Methoden benutzen und nicht immer
zuverlässige, exakte Aussagen liefern.
Deshalb ist es von entscheidendem Vorteil, wenn Agarwal,
Saxena und Kayal 2002 ein Verfahren gefunden haben, das nicht
mehr exponentiell, sondern nur noch in Polynomzeit vom Wert der
zu untersuchenden Primzahl abhängt. Nach diesem Verfahren
ist der Aufwand nicht mehr exponentiell durch (0,1 • ) 10
Stellenzahl der Primzahl / 2 , sondern nur noch durch
Stellenzahl 7,5 beschränkt, d.h.
für eine Primzahl mit 4 Millionen Stellen wären "nur"
etwa 4 000 000 7,5 = 3,3 • 10 49
Rechenoperationen nötig - viel viel weniger als 0,1 •
10 2 000 000 Operationen, aber immer
noch eine riesige, kaum zu bewältigende Zahl: der besagte
Computer würde immer noch rund 10 38 Jahre ( = 10
28 mal das Alter unseres Universums) brauchen. Soweit
die wenig ermutigende Komplexitätstheorie.
Allerdings gibt es für Primzahlen spezieller Bauform (wie
für die oben erwähnten Mersenne-Zahlen oder für
Fermat-Primzahlen) unter Ausnutzung ihrer besonderen Gestalt
deutlich schnellere Verfahren - sonst wären auch mit
verteilter Rechenkraft nicht so viele Mersenne-Primzahlen zu
finden gewesen wie im vorstehenden Abschnitt beschrieben.
Mersenne-Primzahlen können etwa mit dem Lucas/Lehmer-Test
rasch (d.h. binnen Tagen oder Wochen statt in Jahrmilliarden)
geprüft werden (https://de.wikipedia.org/wiki/Mersenne-Primzahl) und
für die Fermat'schen Primzahlen nannte Wikipedia früher
die schnellen Tests nach Pepin oder Suyama, auf die seit Sommer
2014 allerdings nicht mehr verwiesen wird (https://de.wikipedia.org/wiki/Fermat-Zahl).
zum Seitenanfang / zum Seitenende
Endlich Frage zur universellen
Antwort 42 gefunden?
 In seiner 1979
mit dem Buch "Per Anhalter durch die Galaxis" begonnenen
Sciene-Fiction-Reihe berichtet der Autor Douglas Adams (GB 1952 -
USA 2001), dass ein Computer namens "Deep Thought" nach 7,5
Millionen Jahren Rechenzeit endlich die Antwort auf alle Fragen
der Welt gefunden habe - nämlich die Zahl 42. Leider war
über die lange Zeit die genaue Frage vergessen worden (bzw.
war die Aufgabe wohl nie präzise gestellt worden), so dass
man herzlich wenig mit der Antwort anfangen konnte. Zur
Ermittlung der passenden Frage musste erst ein neuer, noch
größerer Computer gebaut werden, der u.a. die gesamte
Erde enthielt - die allerdings wegen einer intergalaktischen
Umgehungsstraße gesprengt wird, kurz bevor der neue
Computer mit seinen Berechnungen fertig war. Die Lösung wird
daher nie gefunden und es bleibt Raum für Spekulationen um
die Bedeutung der 42. Douglas Adams selbst hat nach eigenem
Bekunden die Zahl zufällig ausgewählt und hatte keinen
bestimmten Hintergedanken, auch wenn seither viele Theorien
aufgestellt wurden (s.u., Verweise am Ende dieses Artikels).
In seiner 1979
mit dem Buch "Per Anhalter durch die Galaxis" begonnenen
Sciene-Fiction-Reihe berichtet der Autor Douglas Adams (GB 1952 -
USA 2001), dass ein Computer namens "Deep Thought" nach 7,5
Millionen Jahren Rechenzeit endlich die Antwort auf alle Fragen
der Welt gefunden habe - nämlich die Zahl 42. Leider war
über die lange Zeit die genaue Frage vergessen worden (bzw.
war die Aufgabe wohl nie präzise gestellt worden), so dass
man herzlich wenig mit der Antwort anfangen konnte. Zur
Ermittlung der passenden Frage musste erst ein neuer, noch
größerer Computer gebaut werden, der u.a. die gesamte
Erde enthielt - die allerdings wegen einer intergalaktischen
Umgehungsstraße gesprengt wird, kurz bevor der neue
Computer mit seinen Berechnungen fertig war. Die Lösung wird
daher nie gefunden und es bleibt Raum für Spekulationen um
die Bedeutung der 42. Douglas Adams selbst hat nach eigenem
Bekunden die Zahl zufällig ausgewählt und hatte keinen
bestimmten Hintergedanken, auch wenn seither viele Theorien
aufgestellt wurden (s.u., Verweise am Ende dieses Artikels).
Mitte September 2019 ist es nun gelungen, mit verteilter
Rechenkraft (s.o.) endlich für die
letzte natürliche Zahl z unter 100 die diophantische
Gleichung
(*) a 3 +
b 3 + c 3 = z
zu lösen, d.h. letztlich durch Ausprobieren die ganzen
Zahlen a, b und c zu finden, deren Kubiksumme z ergibt. Angeblich
hat sich der griechische Mathematiker Diophantos von Alexandria
um 250 n.Chr. erstmals mit der Summe dreier Kubikzahlen
beschäftigt (heute bezeichnet man allgemeiner alle Polynome
mit ganzzahligen Koeffizienten und Lösungen als
diophantisch). Während die Lösung von (*) für z =
47 mit betragsmäßig kleinen Zahlen gelingt -
nämlich z.B. a = 6, b = -8 und c = 7, weil
6 3 + (-8) 3 +
7 3 = 47 ist -, sind die Lösungen für
andere Zahlen z oft weitaus größer und viel schwerer
zu finden. Für manche z, nämlich wenn z : 9 den Rest 4
oder 5 ergibt, ist eine Lösungen gänzlich
unmöglich, wie inzwischen bewiesen wurde. Anfang 2019
blieben von den Zahlen z unter 100, die nicht das
Ausschlusskriterium z % 9 = 4 oder z % 9 = 5 erfüllten
(wobei % die Java-Schreibweise für mod[ulo] ist), nur noch
die Zahlen 33 und 42 ohne gefundene Gleichung. Nachdem im April
2019 mit drei 16-stelligen Zahlen eine Lösung für z =
33 ermittelt werden konnte, blieb ausgerechnet die Zahl 42
übrig. Die Antwort z = 42 war sozusagen bekannt, die Frage
bzw. das a, b und c der linken Gleichungsseite musste aber noch
gefunden werden. Ähnlich wie bei Adams gelang das mit
weltumspannender Computerhilfe! Durch den Einsatz von rund einer
halben Million Computern wurde im September 2019 dieses letzte
Rätsel (für z unter 100) mit drei 17-stelligen Zahlen
gelöst: a =
-80 538 738 812 075 974, b =
80 435 758 145 817 515 und c =
12 602 123 297 335 631 erfüllen
zusammen mit z = 42 die Gleichung (*). Jetzt geht die Suche
weiter für z bis 1000. Momentan ist z = 114 die kleinste
Zahl mit bisher unbekannter Lösung (a, b, c).
Zwar ist nun für z = 42 die diophantische Gleichung (*)
gelöst; die "Frage nach dem Leben, dem Universum und dem
ganzen Rest" (Douglas Adams) bleibt hingegen offen. Der Sinn des
Lebens und "von allem" ist wohl kaum eine einfache Gleichung mit
drei dritten Potenzen. Ob es bei der universellen Sinnfrage
hilfreich ist, dass die Antwort 42 dank Deep Thought ja schon
bekannt sein soll?
Wer im Netz weiter suchen will (obwohl dort besser nicht der
Lebenssinn gesucht werden sollte), findet u.a.: einen Bericht
über die Lösung für z=33 bei scinexx, Berichte über die Lösung
für z=42 auf Spiegel online, bei Zeit online oder im kurzen Video im web.de-Magazin sowie Allgemeines über die
"Antwort 42" von D. Adams z.B. auf Wikipedia oder im 10-min-Film auf Youtube (mit vielen angeblichen und echten
Eigenschaften der 42). Theoretische Informatikerinnen und
Informatiker wissen allerdings längst, dass Sinnfragen von
Computern prinzipiell nicht beantwortet werden können - also
auch nicht von Deep Thought oder einem noch so großen
Nachfolger (Nicht mal alle innermathematische Sachverhalte
können berechnet werden, wie z.B. im Artikel Grenzen der Berechenbarkeit auf Schulniveau
erklärt wird).
zum Seitenanfang / zum Seitenende
Rezensionen von Mathe-Software und
-Büchern
Rezensionen von
Mathematik-Software
Im Laufe der Zeit habe ich einige Mathematik-Programme
ausprobiert. Hier meine Meinung zu einigen (älteren)
Angeboten:
a) numerische Programme: Rechen-
und Zeichenhilfen (nit Nachträgen vom
Februar 2025)
- MatheAss 8.0 (B. Schultheiß; für Win)
(jetzt MatheAss 10.0)
- MathProf 2.0 (Riescher; für Win ab 9x)
(inzwischen MathProf 6.0)
- WinFunktion Mathematik plus XII /2002 (St. Polster;
bhv) (jetzt Mathematik alpha)
- Appomatox 3.4.2.0 (F. Schnitzer; für Win ab
9x) (V 3.4.3 noch verfügbar)
b1) interaktive Programme:
Lern- und Übungs- bzw. Nachhilfeprogramme für
die Sekundarstufe I (Klassen 5 - 10)
- Schülerhilfe - 7. Mathe (= Freddy der Fuchs -
Mathematik 7), Aldi Juli/August 2004
- GRIPS! 5. Mathe - Textaufgaben
- Lernpaket Mathematik, Klasse 5 und 6 (= Martins
Lernwerkstatt Mathematik 5&6)
- Multimedia Lernkurs Mathematik Klasse 5-7 (= CD 1
von Lernsoftware Mathematik - Einfach und effektiv -
Klassen 5-10)
- Schülerhilfe Mathe Klasse 7|8
- Aufgabensammlung Geometrie Klasse 8-10
b2) interaktive Programme:
Lern- und Übungs- bzw. Nachhilfeprogramme für
die Sekundarstufe II (Klassen (10,) 11 - 13)
- Mathematik-Baukasten (Franzis)
- Mathematik interaktiv / Telekolleg II: Analysis -
Differentialrechnung (TR Verlagsunion / Rossipaul)
- Differential- und Integralrechnung V 1.1 (Franzis
Multimedia-Mathematik)
- Extremwerte (Hemming Leicht gelernt)
- Mathe Tutor Oberstufe 1 (Maaß/Stöckl;
Koch Media)
- Mathe Tutor Oberstufe 2.0 (Maaß/Stöckl;
Koch Media)
c) Computer-Algebra-Systeme
(CAS): genaues und symbolisches Rechnen, Termumformungen
und Zeichnen
- Die Aufgabe
- Lösung mit Derive 5 / 6
- Lösung mit MuPAD Pro 3.1
- Lösung mit GeoGebra 2.5.1
- Weitere Software und Hinweise
d) Dynamische
Geometrie-Software (DGS). geometrisches Konstruieren,
Abbilden, Bewegen und Messen
- Die vier Aufgaben (Thaleskreis, Strahlensatz,
Kreistangente, Parabelform der Kölnarena)
- Euklid-DynaGeo 2.6e
- GeoGebra 2.5.1
- Zirkel und Lineal 3.71
- Publizieren im Internet bzw. im Schulnetz
- Bezugsquellen und Preise
e) Software zur Linearen
Algebra und zur Vektorgeometrie
- MuPAD und Derive
- MatheAss, WinFunktion Mathematik und MathProf
- Geo(.exe), Vektor / GeoSekII und AG-Analytische
Geometrie
|
Übrigens: Von mir erstellte Software zur Mathematik (wie
den Gleichungssystem-Löser LGS_2, der auch
umgekehrte Kurvendiskussion beherrscht, oder das Programm
WktBaum für die Stochastik in SI und SII)
finden Sie auf meiner "Software"-Seite
!
zum Seitenanfang / zum Seitenende
Eine
Buchbesprechung...
 E.
& M. Niedermair / W. Kassenbrock: Abiturwissen Superbuch --
Mathe & Physik. Der komplette Abiturstoff leicht
verständlich. 576 Seiten. Franzis-Verlag (ISBN
978-3-7723-9265-8) 2009 mit DVD. UVP 29,95 €; im
Februar 2025 für 6,49 € von Medimops im Amazon-Marketplace bzw. als Buch ohne DVD
für 3,86 € von Rebuy bei ebay
E.
& M. Niedermair / W. Kassenbrock: Abiturwissen Superbuch --
Mathe & Physik. Der komplette Abiturstoff leicht
verständlich. 576 Seiten. Franzis-Verlag (ISBN
978-3-7723-9265-8) 2009 mit DVD. UVP 29,95 €; im
Februar 2025 für 6,49 € von Medimops im Amazon-Marketplace bzw. als Buch ohne DVD
für 3,86 € von Rebuy bei ebay
In diesem dicken Buch werden Aufgaben aus dem Oberstufenstoff
der Mathematik (Seiten 29 bis 296) und der Physik (Seiten 297 bis
567) vorgerechnet und gestellt -- aber nicht wirklich
erklärt. Hinweise zum richtigen Lernen und der
Bekämpfung von Prüfungsangst finden sich im ersten,
einführenden Kapitel. Dem Buch von 2008 ist in dieser
Sonderausgabe von 2009 noch eine DVD mit 4 Softwareprodukten
beigegeben: dem lohnenswerten Programm WinMathematik XXL
(einer Lizenzausgabe vom einzeln 30 € teuren MathProf
4.0 -- vgl. meine Besprechung von Mathematik-Software,
Seiten a) und e)) und einer umfangreichen, aber
wenig ansprechenden Mathematik-Aufgabensammlung (belegt 235 MB
auf der Festplatte) sowie zwei schlecht-gemachten Mathematik- und
Physik-Formelsammlungen. Allein WinMathematik XXL lohnt
aber den Preis des Buchs, die (übrigen) Softwareprodukte
kann man zum Glück nach kurzer Prüfung leicht einzeln
deinstallieren.
 Aber
zum Mathematikteil des gedruckten Buches selbst: Er richtet sich
wohl vor allem an Schülerinnen und Schüler, die vor
Klassenarbeiten und/oder den Abiturklausuren typische Aufgaben
üben wollen. Zu den drei Bereichen Analysis (wobei
Exponential- und Logarithmusfunktion sowie die Integralrechnung
eigene Kapitel bekommen haben), zur Linearen Algebra mit
analytischer Geometrie sowie zur Stochastik werden
schulbuch-übliche Aufgaben vorgerechnet, in nachfolgenden
Übungskapiteln findet man weitere kleinere und
größere Aufgabenstellungen zum Selberrechnen mit
anschließender Lösung (z.T. an alte bayrische
Zentralabitur-Aufgaben angelehnt bzw. daher entnommen).
Beeindruckend ist die Breite des abgedeckten Stoffs, gerade auch
in der andernorts oft immer noch stiefmütterlich behandelten
Stochastik. Störend ist hingegen, dass wirklich nur
gerechnet wird und Erklärungen weitestgehend fehlen: so
steht z.B. nirgends, warum man etwa bei der Kurvendiskussion
f ' (x)=0 setzt, um Kandidaten für Extrem- oder
Sattelstellen zu finden. Auch weitere Kriterien werden zwar
gelegentlich benutzt, aber nie erläutert (der Abschnitt 2.5
'Grundlagen zur Kurvendiskussion' hat daher den Namen nicht
verdient, auch wenn es dort einige Definitionsmengen-,
Symmetrie-, Tangenten- und Nullstellenbestimmungen sowie
Beispiel-Diskussionen für je eine ganzrationale,
gebrochenrationale und trigonometrische Funktion gibt -- aber
eben keine Grundlagen). Ähnliches gilt auch für alle
anderen Kapitel und Themen. Insofern eignet sich das Buch
wirklich nur für Schülerinnen und Schüler, die
für Erklärungen und zum Verständnis auf andere
Quellen zugreifen können und hier nur das rezepthafte
Durchrechnen sehen und üben wollen (auch die
Aufgabensammlung auf DVD liefert als Kontroll-Lösungen immer
nur eine Folge unkommentierter Rechenschritte) -- oder für
Lehrerinnen und Lehrer als Materialvorrat für weitere
(Haus-)Aufgaben zusätzlich zum Schulbuch. Zur Vorbereitung
auf mündliche Prüfungen oder um den Sinn der Verfahren
einzusehen, eignet sich dieses Buch nicht! Der Untertitel des
Buchs "Der komplette Abiturstoff leicht verständlich" ist
insofern irreführend.
Aber
zum Mathematikteil des gedruckten Buches selbst: Er richtet sich
wohl vor allem an Schülerinnen und Schüler, die vor
Klassenarbeiten und/oder den Abiturklausuren typische Aufgaben
üben wollen. Zu den drei Bereichen Analysis (wobei
Exponential- und Logarithmusfunktion sowie die Integralrechnung
eigene Kapitel bekommen haben), zur Linearen Algebra mit
analytischer Geometrie sowie zur Stochastik werden
schulbuch-übliche Aufgaben vorgerechnet, in nachfolgenden
Übungskapiteln findet man weitere kleinere und
größere Aufgabenstellungen zum Selberrechnen mit
anschließender Lösung (z.T. an alte bayrische
Zentralabitur-Aufgaben angelehnt bzw. daher entnommen).
Beeindruckend ist die Breite des abgedeckten Stoffs, gerade auch
in der andernorts oft immer noch stiefmütterlich behandelten
Stochastik. Störend ist hingegen, dass wirklich nur
gerechnet wird und Erklärungen weitestgehend fehlen: so
steht z.B. nirgends, warum man etwa bei der Kurvendiskussion
f ' (x)=0 setzt, um Kandidaten für Extrem- oder
Sattelstellen zu finden. Auch weitere Kriterien werden zwar
gelegentlich benutzt, aber nie erläutert (der Abschnitt 2.5
'Grundlagen zur Kurvendiskussion' hat daher den Namen nicht
verdient, auch wenn es dort einige Definitionsmengen-,
Symmetrie-, Tangenten- und Nullstellenbestimmungen sowie
Beispiel-Diskussionen für je eine ganzrationale,
gebrochenrationale und trigonometrische Funktion gibt -- aber
eben keine Grundlagen). Ähnliches gilt auch für alle
anderen Kapitel und Themen. Insofern eignet sich das Buch
wirklich nur für Schülerinnen und Schüler, die
für Erklärungen und zum Verständnis auf andere
Quellen zugreifen können und hier nur das rezepthafte
Durchrechnen sehen und üben wollen (auch die
Aufgabensammlung auf DVD liefert als Kontroll-Lösungen immer
nur eine Folge unkommentierter Rechenschritte) -- oder für
Lehrerinnen und Lehrer als Materialvorrat für weitere
(Haus-)Aufgaben zusätzlich zum Schulbuch. Zur Vorbereitung
auf mündliche Prüfungen oder um den Sinn der Verfahren
einzusehen, eignet sich dieses Buch nicht! Der Untertitel des
Buchs "Der komplette Abiturstoff leicht verständlich" ist
insofern irreführend.
(Im Vorwort zum Physikteil steht übrigens viel deutlicher:
"Es ist kein Physikbuch im herkömmlichen Sinn. Es werden nur
sehr bedingt .. Zusammenhänge hergeleitet oder bewiesen...
Die Stärke dieses Buches liegt vielmehr in der sehr
komprimierten Darstellung .. und in den Übungsaufgaben
einschließlich der zugehörigen Musterlösungen"
(S. 299))
Außerdem orientiert sich das Buch am traditionellen
bayrischen und baden-württembergischen Abitur. Für
Nordrhein-Westfalen fehlen anwendungsorientierte(re)
Mathematik-Aufgaben. An Themen fehlen in der Linearen Algebra
z.B. Übergangsmatrizen und in der Stochastik ist das Kapitel
Unabhängigkeit mit weniger als einer Dreiviertelseite und
ohne Satz von Bayes viel zu dürftig behandelt. Und das
Stichwortverzeichnis enthält zu wenige Einträge, um bei
vielen Suchen wirklich zu helfen.
Noch ein Wort zu Fehlern: Grundsätzlich waren die Autoren
nicht nur fleißig, sondern scheinen sich auch Mühe
gegeben zu haben. Natürlich gibt es trotzdem Fehler. Wenn im
Wahrscheinlichkeits-Baum (auf S. 160) bei einem Ast der Strich
und die Angabe der Wahrscheinlichkeit fehlt, so ist das (wie bei
einigen offensichtlichen Tippfehlern) sicher leichter zu
verschmerzen, als wenn an vielen Stellen die benötigten
Klammern weggelassen werden (z.B. auch S. 109) und gar in allen
Beispielen zur Polynomdivision immer z.B. - x2+3x
falsch an Stelle des richtigen Terms -(x2+3x) =
-x2-3x steht (Seiten 53 bis 55). Allerdings sind
Fehler zum Glück seltener als etwa in "Physik espresso!" aus
dem gleichen Verlag (siehe Besprechung auf meiner Physik-Webseite) und seltener
als in den Lösungsbüchern für die Lehrerhand der
meisten Schulbuchverlage -- auch wenn Thomas Beneken als "ein
besorgter Vater" durchaus nachvollziehbar wegen der von ihm schon
auf den ersten Seiten gefundenen Unzulänglichkeiten in
seiner kritischen Rezension bei amazon.de vom Buch
gänzlich abrät
Bei einem Preis von unter 10 € und wegen der
empfehlenswerten Software WinMathematik XXL halte ich --
unter den dargestellten Einschränkungen bzw. für den
genannten Zweck -- den Kauf der Ausgabe mit DVD trotzdem für
berechtigt. Über den Physikteil und die Formelsammlungen
berichte ich zusätzlich auf meine "Physik"-Seite.
zum Seitenanfang / zum Seitenende
...und noch ein
Buchtipp
 Georg Glaeser: Der
mathematische Werkzeugkasten - Anwendungen in Natur und
Technik. Jokers edition 2007 (378 Seiten) für 12,95
€. [Die hier besprochenen Ausgabe, basierend auf der
Auflage von 2004, gibt's allenfalls noch gebraucht. Seit
September 2021 ist die wesentlich erweiterte, jetzt 583 Seiten
umfassende 5. Auflage zum Preis von 34,99€ aktuell]
Georg Glaeser: Der
mathematische Werkzeugkasten - Anwendungen in Natur und
Technik. Jokers edition 2007 (378 Seiten) für 12,95
€. [Die hier besprochenen Ausgabe, basierend auf der
Auflage von 2004, gibt's allenfalls noch gebraucht. Seit
September 2021 ist die wesentlich erweiterte, jetzt 583 Seiten
umfassende 5. Auflage zum Preis von 34,99€ aktuell]
Dieses Buch sei jeder Mathematik-Lehrerin und jedem
Mathematik-Lehrer, aber auch allen interessierten
Oberstufenschülerinnen und -schülern an Herz gelegt.
Einer groben mathematischen Fachsystematik folgend, bietet das
Buch in 7 Kapiteln (von einfachen Gleichungen aus der Mittelstufe
über einfache Geometrie und Trigonometrie bis zur Analysis
und Vektorrechnung der Oberstufe) und zwei Anhängen (zu
Zahlen und Musik) und in insgesamt über 50 Abschnitten eine
Fülle von Anwendungen: Nach einer sehr kurzen mathematischen
Einleitung werden prägnante Beispiele aufgeführt und
mit den gerade vorgestellten mathematischen Mitteln
behandelt.
Das Gelungene ist die Auswahl der Beispiele: Sei es die
durchschnittliche Erosion des Tafelbergs pro Jahr, der
Durchmesser eines Moleküls, die Schärfentiefe bei
Digitalaufnahmen, die Verzögerung beim Bungy-Jumping, der
Grund für dünne Spinnenbeine und dicke Säulenbeine
beim Elefanten, die Ausrichtung von Sonnenspiegeln, das
Maximalgewicht eines flugfähigen Vogels (oder auch
Flugsauriers), die Planetenbewegung oder das Aufwickeln eines
Taus: Mehrere Hundert Anwendungen werden erfrischend knapp aber
klar vorgestellt und kurz durchgerechnet. Die willkürlich
herausgegriffene abgebildete Doppelseite zeigt den typischen
Aufbau des Buchs, das (bei mathematischer Vorbildung) durchaus
auch als nicht zu schwierige Urlaubslektüre geeignet ist.
Der Lehrer erhält eine Menge an Anregungen; allerdings
bleibt es ihm überlassen, die hier jeweils nur kurz
umrissenen Beispiele so aufzubereiten, dass sie auch zum Einsteig
oder zur Motivation der benötigten Rechenwege und -verfahren
im Schulunterricht dienen. Insofern unterschiedet sich der Ansatz
hier von dem der Blikk-Webseiten oder dem der MUED (siehe weiter
unten auf dieser Seite). Trotzdem und besonders für den
günstigen Preis kann ich das Buch nur empfehlen: ich habe es
gern und mit Gewinn gelesen!

Allerdings geht der Verlag wohl zu weit, wenn er das Buch auch
als Einstieg in die Mathematik empfiehlt. Obwohl durch die
mathematische Einleitung am Anfang jeden Abschnitts das
Handwerkszeug für die folgenden Beispiele kurz vorgestellt
wird, dürfte ein völliger Laie mit der formalen
Lösung anschließend doch überfordert sein. Etwas
mathematische Vorbildung sollte wohl besser mitgebracht
werden.
zum Seitenanfang / zum Seitenende
3.
Buchbesprechung: Stochastik-Fehler
 Alex Reinhart: Statistics done wrong -
Deutsche Ausgabe: Statistik richtig anwenden und Fehler
vermeiden. 208 Seiten. mitp-Verlag 2016. ISBN
978-3-95845-252-7. Originalpreis 24,99 €
inzwischen aufgehoben;
bei mitp im Februar 2024 schon für knapp 4
€.
Alex Reinhart: Statistics done wrong -
Deutsche Ausgabe: Statistik richtig anwenden und Fehler
vermeiden. 208 Seiten. mitp-Verlag 2016. ISBN
978-3-95845-252-7. Originalpreis 24,99 €
inzwischen aufgehoben;
bei mitp im Februar 2024 schon für knapp 4
€.
Zunächst hatte
ich mich bei diesem aus dem Amerikanischen übersetzten Buch
gewundert, warum immer nur vom p-Wert statt von der
Irrtumswahrscheinlichkeit oder dem Signifikanzniveau von
Hypothesentests geredet wurde. Kannte der Übersetzer nicht
die bei uns üblichen Begriffe? Schnell wurde aber klar, dass
dahinter Absicht steckt. Der Autor will grundlegende
Irrtümer im Umgang mit der Stochastik aufdecken. Dazu
gehört der Kampf gegen den verbreiteten Glauben, eine auf
Grund eines Hypothesentests mit einem p-Wert von 5 %
getroffene Aussage sei mit 95-%-iger Wahrscheinlichkeit richtig.
5 % ist aber nur die Wahrscheinlichkeit für die
irrtümliche Ablehnung der Nullhypothese. Wie sicher dann -
wenn z.B. die Nullhypothese H0: „kein
Brustkrebs" mit höchstens 5 % Irrtumswahrscheinlichkeit
für den Fehler 1. Art abgelehnt werden kann - das Gegenteil,
nämlich die Diagnose Brustkrebs, zutrifft, hängt aber
von weiteren Bedingungen ab: u.a. davon, wie groß der
Fehler 2. Art des Tests ist, und wie verbreitet Brustkrebs
überhaupt ist (Prävalenz). Das führt dazu, dass
auch viele Frauen ohne Brustkrebs eine falsche positive Diagnose
kriegen. Auch wenn fast alle Erkrankten tatsächlich erkannt
werden, haben dadurch im Buchbeispiel (S. 73) tatsächlich
nur 9 % der Frauen mit (angeblich fast sicherer)
Brustkrebsdiagnose tatsächlich einen Tumor - also nur
9 % statt vermeintlich 95 % Sicherheit! Entsprechend
verzichtet Reinhart auf irreführenden
Sprachgebrauch.
Obwohl es für
Brustkrebs inzwischen bei den Mammografie-Instituten
Aufklärungsblätter gibt, die anschaulich und korrekt
die (begrenzte) Aussagekraft der Untersuchung erklären,
interpretiert die Mehrzahl der Ärzte solche Ergebnisse
falsch. Allgemein sind die meisten Fachleute kaum in der Lage,
die Ergebnisse von Untersuchungen in ihrem Fach richtig zu
deuten.
Darüber hinaus
sind schon viele veröffentlichte Daten falsch oder zumindest
fragwürdig, weil die Autoren die statistischen Werkzeuge
nicht richtig oder sinnvoll anzuwenden wussten. An diese Gruppe -
Studenten und Forscher im medizinischen, biomedizinischen und
psychologischen Bereich - wendet sich der Autor
hauptsächlich. Im Buch werden viele mögliche Fehler --
nichtsignifikante Unterschiede der Signifikanz, zirkuläre
Analysen, falscher Umgang mit Testabbrechern, Regression zur
Mitte, überflüssige Zweiteilung, Simpson-Paradoxon,
voreingenommene Berichterstattung, Nichtveröffentlichung
klinischer Studien ohne signifikantes Ergebnis, usw. -- oft mit
Beispielen angesprochen. Allerdings werden die Beispiele nicht
von Grund auf durchgerechnet. Der Autor (selbst Statistiker an
einer Uni) wendet sich an eine Leserschaft, die schon z.B. durch
ein oder zwei Semester Statistikkurse Vorkenntnisse hat und die
Verfahren und den Umgang mit Statistik-Programmpaketen wie z.B.
SPSS im Prinzip kennt. Allerdings hält er die übliche
Statistikausbildung z.B. der Mediziner an den Universitäten
für unzureichend, da sie nicht geeignet sei,
persönliche Fehlvorstellungen abzubauen. Offenbar sind seit
rund 50 Jahren immer noch die gleichen Fehler weit verbreitet
(vgl. auch meinen vorigen Abschnitt "Wissenschaftskrise u.a.
wegen falsch verstandener Hypothesentests")!
Reinharts Tipps
für bessere Kurse bzw. besseren Unterricht, der Lernende
zwingt, ihre Ansichten zunächst klar zu äußern
und sich (erst) danach mit dem richtigen Weg soweit auseinander
zu setzen, sodass Diskrepanzen erkannt und falsche Auffassungen
dauerhaft korrigiert werden, sind für Dozenten und auch
Lehrer durchaus interessant. Seinem Appell, wichtige
Untersuchungen immer von einem ausgebildeten Statistiker
begleiten zu lassen, kann man nur zustimmen - ebenso dem Wunsch,
statt Testergebnisse der Art „mit p-Wert 5% besser als das
Placebo (bzw. die Standardarznei)" lieber Konfidenzintervalle
für die neue Wirksamkeit in der Form „lässt 19 %
bis 48 % der Erkrankten innerhalb 1 Woche genesen" anzugeben. Die
Breite des Intervalls macht auch die (Un-)Sicherheit der Aussage
deutlich. Außerdem plädiert er für die
Vorab-Berechnung und Angabe der Teststärke sowie für
die Veröffentlichung aller (Roh-)Daten z.B. auf geeigneten
Internet-Servern, um Studien überprüf- bzw.
nachvollziehbar zu machen.
Auch wenn man
Einiges über Medikamententests erfährt und gute Tipps
erhält: Wegen der abweichenden Zielgruppe und des
vorausgesetzten Wissens ist das Buch für die Schule nur
bedingt geeignet; beim reduzierten Preis für Studium und
Praxis aber dringend zu empfehlen.
Hinweis:
Die oft problematische, ja unverständige Verwendung
stochastischer Methoden habe ich weiter oben auf dieser Seite im
"Stochastik"-Kapitel bereits erwähnt, z.B. im Abschnitt
"Wissenschaftskrise u.a. wegen
falschverstandener Hypothesentests".
Eine Anleitung zum richtigen Testen findet sich zuvor als kurzes
Übersichtsblatt 'Richtiges_Hypothesentesten.pdf' oder
ausführlicher im längeren Referat 'stoch-s2.pdf' im
Abschnitt "Stochastik in der
SII".
zum Seitenanfang / zum Seitenende
Verweise
Bevor Sie einen der folgenden Verweise anklicken, sollten Sie
erst meine Seite zu Ihren Favoriten oder Lesezeichen
hinzufügen, damit Sie anschließend sicher hierher
zurück finden. Natürlich kann ich für den Inhalt
fremder Seiten keine Verantwortung übernehmen. Wenn ein
Verweis nicht funktioniert, dort inzwischen andere Inhalte sind
oder wenn Sie mir weitere gute Seiten empfehlen können,
bitte ich um eine kurze Nachricht. Letzte Aktualisierung im Februar
2025, wobei ich auch einige Verweise ('Links') ganz
entfernen müssen, weil die ursprünglichen Betreiber -
oft Lehrer, die jetzt im Ruhestand sind - ihre Materialien nicht
mehr anbieten bzw. ihre Webpräsenz aufgegeben haben.
Hinweis: die fremden Seiten werden in einem neuen
Browser-Fenster geöffnet. Geschieht beim Anklicken eines
Verweises scheinbar nichts, wird das neue Fenster vermutlich vom
aktuellen Fenster verdeckt -- bitte per Task-Leiste ins neue
Fenster wechseln!
MUNDO.Schule
|
Eine neue, offene,
staatlich geförderte Bildungsmediathek der Länder
mit anschaulichen Materialien zu mehreren Fächern, u.a,
Physik (1171), Mathematik (1042) oder Informatik (82 -
jeweils Stand Okt. 2020) |
| Mathe-Werkstatt |
Herr Elschenbroich
bietet auf seiner Homepage viel Interessantes zur und rund um
die Mathematik (seit 2012 nicht mehr aktualisiert). |
| MUED e.V. |
Anwendungs- und
handlungsorientierte Mathematik. Mehr über diesen Verein
weiter oben auf dieser Seite. |
| Reale Probleme modellieren mit Mathe |
Die Links
führen zum SII- bzw. SI-Mathematik-Bereich von blikk,
einem umfangreichen und lohnenswerten Webangebot mit
vielfältigen Anregungen, Mathematik aus realen
Beispielen zu extrahieren. |
| MatheÜberall |
| Wisweb |
Interessant ist auf
jeden Fall auch der niederländische Ansatz
kontextbezogener Mathematik. Kern der Wisweb-Seite waren
zahlreichen Applets, die - nach Anmeldung - zum interaktiven
Entdecken der Mathematik anleiten sollten. Inzwischen wurde
die Seite umgestaltet, und ist nicht mehr in deutsch, sondern
nur noch in niederländisch und englisch
verfügbar. |
| MatheOnline Hintergründe |
Umfangreiche
Materialien der Uni Wien, nach Themengebieten und
Unterrichtsgegenständen geordnet. Zusätzliche
Verzweigungen zu einem mathem. Lexikon, zu Online-Werkzeugen
(siehe auch unten: Online-Berechnungen und Mathepower), zur
Galerie von Java-Applets,... |
| emath.de |
Rainer Müller
stellt - inzwischen oft kostenpflichtig -
Zentral-Abi-Aufgaben mit Lösungen vor, erlaubt das
Herunterladen eines Abi-Vorbereitungskurses ("Know-How"),
bietet online-Berechnungen bzw. Freeware-Tools (unter
'Lernsoftware Mathematik', schön: "Geo" für die
Analytische Geometrie) und moderiert ein Forum
("Mathe-Board") für mathematische Fragen |
| Arne
Madincea |
Internetseiten eines
Berliner Mathelehrers, der Unterrichtsmaterial und
Abiturvorschläge zum Download bereit stellt (seit 2012
offenbar nicht mehr aktualisiert) |
| Tino Hempel |
Viele Tipps zur
Mathematik, aber auch zu Informatik und Physik finden sich
auf dieser Seite eines Lehrers |
| MathePrisma |
Zu vielen
mathematischen Themen und einigen Informatikbereichen
hält die Uni Wuppertal schöne mehrseitige
interaktive Module zum Online-Lernen oder auch zum Download
bereit |
formelsammlung-mathe.de
|
Herr Schmidt-Voigt
präsentiert knapp, aber übersichtlich einige
wichtige Formeln. Abgerundet wird das Angebot durch einen
schwachen Online-Taschenrechner und einen schöneren
Online-Prozentrechner. Werbung über einen
verprovisionierten Partner-Link zu Amazon für den Kauf
der "Formelsammlungen für Schule und Studium" in
Buchform |
Mathebibel.de
|
Hier erklärt
Andreas Schneider viele Begriffe und Verfahren aus allen
Bereichen der Mathematik. Seine Erläuterungen sollten
den meisten Schülerinnen und Schülern wirklich
weiter helfen können, sodass Mathematik auch online
gelernt werden kann! Werbung für Easy-Tutor. |
| bruchrechnen-kapiert |
Auf dieser Seite findet
man Regeln, Beispiele, einen Online-Bruchrechner und
interaktive Aufgaben zum Thema Bruchrechnen -- und leider
auch viel Werbung für fremde Seiten, womit das sonst
gelungene und ambitionierte Angebot offenbar finanziert
wird. |
| SMART |
Eine Datenbank (bis
2015 gepflegt von der Uni Bayreuth, aber noch verfügbar)
mit über 5500 Mathe- und Physik-Aufgaben bietet
Beispiele zu fast jedem Schulthema (Gymnasium und
Realschule) |
| DWU-Unterrichtsmaterialien |
Unterrichtsmaterialien
für Mathematik (über 430 Seiten) und Physik (mehr
als 300 Seiten) von Dieter Welz, inzwischen wieder auf seiner
privaten Webseite |
| ZUM-Mathematik |
Fachportal Mathematik
der Zentrale für Unterrichtsmaterialen. Außerdem
dort erreichbar: Wiki über digitale Mathematik |
| GeoGebra |
Unter 'Materialien'
sind angeblich über 1 Million GeoGebra-Konstruktionen, Simulationen und
GeoGebra-bezogenene Unterrichtsmaterialien zu finden, die zum
Glück gut katalogisiert sind, sodass sich wahre
Schätze finden lassen. (Die GeoGebra-Version 2.5 habe
ich übrigens oben auf meinen
Software-Rezensions-Seiten c) und d)
vorgestellt -- inzwischen [d.h. im März 2020] gibt's
neben vielen neueren Apps unter 'Offline Apps'/'Apps
herunterladen' mit Geogebra Classic 6 das neueste
Gesamtpaket. |
| Z.u.L.-Beispiele u. -Anwendungen |
Hier finden sich einige
schöne Anwendungen zum Geometrie-Programm Zirkel
und Lineal (Z.u.L.) -- mit Verweisen auf weitere
Material-Seiten. (Auch Z.u.L. habe ich in einer älteren
Version oben auf meiner
Software-Rezensions-Seite d) vorgestellt). |
| witze1, witze2, .. |
Hier wird gezeigt, dass
Mathe keineswegs humorlos ist! |
| arndt-bruenner |
Die hervorragend
gemachten Mathe-Seiten von Arndt Brünner kombinieren
meist interaktive Berechnungen oder Grafikdarstellungen
für unzählige Aufgaben und Fragestellungen mit
Theorie bzw. mit Erklärungen zu den eingesetzten
Verfahren. Manchmal sind auch umfangreiche Lehrtexte mit
vorgerechneten Beispielen mit Übungsaufgaben kombiniert,
wo eingetippte Lösungen geprüft werden können.
Neben dem meist verwendeten Javascript kommen auch einige
Java-Applets zum Einsatz. |
| Online-Berechnungen |
Übersicht
über Seiten, wo online eingetippte Funktionsterme
algebraisch differenziert, integriert oder gezeichnet werden
können; Verweise auf Gleichungslöser und
anspruchsvolle numerische oder algebraische Bestimmungen;
dynamische Geometrie (siehe auch oben: MatheOnline
Hintergründe und emath, sowie den folgenden Link:
Mathepower) -- gut gepflegt von Bildungseinrichtungen in
Österreich |
| Omni-Calculator (am./engl.) |
 ein Portal, das
gezielten Zugang zu über 3700 kostenlosen
Online-Rechnern aus allen Wissenschafts- und Lebensbereichen
bietet - allerdings alles nur in englischer Sprache. ein Portal, das
gezielten Zugang zu über 3700 kostenlosen
Online-Rechnern aus allen Wissenschafts- und Lebensbereichen
bietet - allerdings alles nur in englischer Sprache. |
| Mathepower |
Kostenlose
Online-Berechnungen für die typischen Mathe-Aufgaben der
1. bis 10. Klasse (deutsch) - vielfach, z.B. beim Lösen
quadrat. Gleichungen, werden außer dem Ergebnis auch
die algebraischen Umformungsschritte angezeigt.
Gelungen! |
| Mathematik
Online |
Früher mal eine
Art FAQ zur Mathematik -- Antworten zu einigen (recht
willkürlich) ausgewählten Fragen zur und über
die Mathematik -- ist die Seite inzwischen offenbar nur noch
eine Linkliste zu weiteren Mathe-Seiten |
| matheboard.de |
An
diesem "Schwarzen Brett" kann jeder Fragen zur Mathematik
'posten' (aufschreiben und aushängen), die dann von
anderen Besucherinnen und Besuchern der Seite beantwortet
werden - mal gut, mal weniger gut. Meist erhält man
mehrere Antworten. Natürlich kann man auch selbst auf
andere Fragen antworten. Ebenfalls vorhanden: Boards zu
Physik und Latein! |
| Mathe-CD |
In diesem ehrgeizigen
Projekt werden Tausende schultypischer Mathe-Aufgaben
zusammen getragen. Auch wenn nur ein kleiner Teil kostenlos
sichtbar ist (für den Rest soll die CD gekauft werden),
reicht auch das schon für viele Übungen! |
| Känguru |
Der Mathe-Wettbewerb
mit den meisten Teilnehmern (ab der Unterstufe!) |
| math4u |
Mehr als 470 Aufgaben
(gesammelt bis 2001), um auf Mathe-Wettbewerbe und
-Olympiaden vorzubereiten |
| Zahlenjagd |
Eine
österreichische Seite mit einem Sammelsurium zur
Mathematik, u.a. Facharbeiten und Rätseln |
| Wurzel |
Auch der Verein Wurzel
e.V. aus Jena, der die gleichnamige monatliche Zeitschrift
für mathematisch interessierte Schüler heraus gibt,
hält auf der Webseite u.a. einige Knobeleien bereit |
| Mathe-Rätsel |
Ingmar Rubin bietet
einige ziemlich anspruchsvolle Mathe-Aufgaben; die Sammlung
wurde schon länger nicht mehr aktualisiert |
| Mathworld |
Eric Weissteins
anspruchsvolle mathematische Schatzkiste (engl.) |
| claymath.org |
Großes Geld
verdienen mit Mathe? Für die Lösung von sieben so
genannter Millenium-Probleme sind Preisgelder von je
1.000.000 $ ausgesetzt! (engl.) |
|
Peanut-Software
Version 1996 auf australischer Seite
Version 2000 auf italienischer
Seite
Version 2012 auf
web.archive.org/web/20121208065328/http://math.exeter.edu/rparris
(möglicherweise mit Virus, daher nicht verlinkt)
|
Einige sehr schöne
kostenlose Mathe-Programme (u.a. für Funktionsgraphen,
Matrizenrechnung, Stochastik, Fraktale, Berechnung aller
Stellen von beliebig großen Zahlen,..) stammen vom 2012
verstorbenen Rick Parris und waren auf der Webseite
math.exeter.edu/rparris seiner Wirkungsstätte in den USA
verfügbar. Die Seite wurde inzwischen gelöscht.
Zwar finden sich ältere Versionen seiner
Übersichtsseite auch auf den nebenstehend genannten
Servern, allerdings sind die Programme dort nicht hinterlegt,
d.h. die Download-Links führen meist ins Leere.
Allerdings kann nach den Programmnamen gesucht werden; so
fand ich im Februar 2024 noch z.B.wp32z.exe (Winplot) auf
Softfamous oder auch auf softpedia. Eine Oberfläche zu allen
Programmen gibts noch auf howe-two.com. Zu Winplot findet sich auch 2024
eine ausführliche engl. Anleitung auf einer hawaiianischen Webseite. |
| Software-Download bzw.Download-Übersicht |
Meine Programme zum
Herunterladen, u.a. WktBaum (Stochastik), LGS_2
(Gleichungssysteme und Umgekehrte Kurvendiskussion),
Sin&Cos (Trigonometrie) sowie Informatik-Programme. (Mehr
Mathematik-Unterrichtsmaterial
gibt's weiter oben auf dieser Seite, ansonsten auch auf
meiner Informatikseite ) |
Weitere Verknüpfungen (z.B. mit Bildungsservern,
Schulbuchverlagen, Hausarbeiten, Referaten usw.) bei den
Verweisen auf meiner Seite & mehr
 Hinweise auf regelmäßige
Mathematik-Wettbewerbe mit den
Terminen für 2025 (2026 wohl ähnlich)
Hinweise auf regelmäßige
Mathematik-Wettbewerbe mit den
Terminen für 2025 (2026 wohl ähnlich) Am 1. Dezember 2025 ging es wieder
los: Nach einmaliger Anmeldung konnte man die eigenen
Lösungen täglich per eMail einsenden und damit auf
einen der vielen Gewinne hoffen, die auf die Teilnehmerinnen und
Teilnehmer warten. Aber auch ohne Registrierung kann man - auch
jetzt, nachträglich noch - bei den meisten Angeboten
Türchen öffnen und die Fragen sehen und beantworten.
Denn auch ohne Gewinnchance macht das Rätseln Spaß.
Wer trotzdem auch materielle Preise gewinnen will, sollte sich im
November 2026 für den kommenden Advent anmelden. Und um die
Gewinnchancen zu erhöhen, übt man jetzt am besten schon
an den alten Aufgaben!
Am 1. Dezember 2025 ging es wieder
los: Nach einmaliger Anmeldung konnte man die eigenen
Lösungen täglich per eMail einsenden und damit auf
einen der vielen Gewinne hoffen, die auf die Teilnehmerinnen und
Teilnehmer warten. Aber auch ohne Registrierung kann man - auch
jetzt, nachträglich noch - bei den meisten Angeboten
Türchen öffnen und die Fragen sehen und beantworten.
Denn auch ohne Gewinnchance macht das Rätseln Spaß.
Wer trotzdem auch materielle Preise gewinnen will, sollte sich im
November 2026 für den kommenden Advent anmelden. Und um die
Gewinnchancen zu erhöhen, übt man jetzt am besten schon
an den alten Aufgaben! Vor
Längerem habe ich irgendwo mal die Schlagzeile gelesen:
"Erdmännchen können Vektorrechnung!".
Tatsächlich hatte man Erdmännchen in einem neuen,
unübersichtlichen Gelände zur Höhle A gebracht.
Dann wurden sie mit Futter zu einem entfernten Punkt B und
schließlich von dort zum Punkt C gelockt. Nach der
Fütterung hatte man die poussierlichen Tierchen sich
selbst überlassen, die schließlich zur Höhle A
zurück kehrten -- aber überwiegend nicht mit dem
Umweg über B, sondern indem sie einen direkten Weg suchten
und fanden. Allerdings dürfte es etwas übertrieben
sein, hieraus auf die Beherrschung der Vektorrechnung und ein
tiefes Verständnis von Linearer Algebra zu
schließen. Aber die Tiere haben offenbar eine gute
Raumvorstellung bzw. eine 'inneren Karte'.
Vor
Längerem habe ich irgendwo mal die Schlagzeile gelesen:
"Erdmännchen können Vektorrechnung!".
Tatsächlich hatte man Erdmännchen in einem neuen,
unübersichtlichen Gelände zur Höhle A gebracht.
Dann wurden sie mit Futter zu einem entfernten Punkt B und
schließlich von dort zum Punkt C gelockt. Nach der
Fütterung hatte man die poussierlichen Tierchen sich
selbst überlassen, die schließlich zur Höhle A
zurück kehrten -- aber überwiegend nicht mit dem
Umweg über B, sondern indem sie einen direkten Weg suchten
und fanden. Allerdings dürfte es etwas übertrieben
sein, hieraus auf die Beherrschung der Vektorrechnung und ein
tiefes Verständnis von Linearer Algebra zu
schließen. Aber die Tiere haben offenbar eine gute
Raumvorstellung bzw. eine 'inneren Karte'.
 Kombinatorik
& Graphenthe
Kombinatorik
& Graphenthe


 Anfang Juli 2020 konnte man
vielerorts lesen (online u.a. bei
Anfang Juli 2020 konnte man
vielerorts lesen (online u.a. bei 
 Wahrscheinlich wurde zur Ermittlung der Formeln ein
Mathematik-Programm wie z.B.
Wahrscheinlich wurde zur Ermittlung der Formeln ein
Mathematik-Programm wie z.B. 
 E.
& M. Niedermair / W. Kassenbrock: Abiturwissen Superbuch --
Mathe & Physik. Der komplette Abiturstoff leicht
verständlich. 576 Seiten. Franzis-Verlag (ISBN
978-3-7723-9265-8) 2009 mit DVD. UVP 29,95 €; im
Februar 2025 für 6,49 € von Medimops im
E.
& M. Niedermair / W. Kassenbrock: Abiturwissen Superbuch --
Mathe & Physik. Der komplette Abiturstoff leicht
verständlich. 576 Seiten. Franzis-Verlag (ISBN
978-3-7723-9265-8) 2009 mit DVD. UVP 29,95 €; im
Februar 2025 für 6,49 € von Medimops im  Aber
zum Mathematikteil des gedruckten Buches selbst: Er richtet sich
wohl vor allem an Schülerinnen und Schüler, die vor
Klassenarbeiten und/oder den Abiturklausuren typische Aufgaben
üben wollen. Zu den drei Bereichen Analysis (wobei
Exponential- und Logarithmusfunktion sowie die Integralrechnung
eigene Kapitel bekommen haben), zur Linearen Algebra mit
analytischer Geometrie sowie zur Stochastik werden
schulbuch-übliche Aufgaben vorgerechnet, in nachfolgenden
Übungskapiteln findet man weitere kleinere und
größere Aufgabenstellungen zum Selberrechnen mit
anschließender Lösung (z.T. an alte bayrische
Zentralabitur-Aufgaben angelehnt bzw. daher entnommen).
Beeindruckend ist die Breite des abgedeckten Stoffs, gerade auch
in der andernorts oft immer noch stiefmütterlich behandelten
Stochastik. Störend ist hingegen, dass wirklich nur
gerechnet wird und Erklärungen weitestgehend fehlen: so
steht z.B. nirgends, warum man etwa bei der Kurvendiskussion
f ' (x)=0 setzt, um Kandidaten für Extrem- oder
Sattelstellen zu finden. Auch weitere Kriterien werden zwar
gelegentlich benutzt, aber nie erläutert (der Abschnitt 2.5
'Grundlagen zur Kurvendiskussion' hat daher den Namen nicht
verdient, auch wenn es dort einige Definitionsmengen-,
Symmetrie-, Tangenten- und Nullstellenbestimmungen sowie
Beispiel-Diskussionen für je eine ganzrationale,
gebrochenrationale und trigonometrische Funktion gibt -- aber
eben keine Grundlagen). Ähnliches gilt auch für alle
anderen Kapitel und Themen. Insofern eignet sich das Buch
wirklich nur für Schülerinnen und Schüler, die
für Erklärungen und zum Verständnis auf andere
Quellen zugreifen können und hier nur das rezepthafte
Durchrechnen sehen und üben wollen (auch die
Aufgabensammlung auf DVD liefert als Kontroll-Lösungen immer
nur eine Folge unkommentierter Rechenschritte) -- oder für
Lehrerinnen und Lehrer als Materialvorrat für weitere
(Haus-)Aufgaben zusätzlich zum Schulbuch. Zur Vorbereitung
auf mündliche Prüfungen oder um den Sinn der Verfahren
einzusehen, eignet sich dieses Buch nicht! Der Untertitel des
Buchs "Der komplette Abiturstoff leicht verständlich" ist
insofern irreführend.
Aber
zum Mathematikteil des gedruckten Buches selbst: Er richtet sich
wohl vor allem an Schülerinnen und Schüler, die vor
Klassenarbeiten und/oder den Abiturklausuren typische Aufgaben
üben wollen. Zu den drei Bereichen Analysis (wobei
Exponential- und Logarithmusfunktion sowie die Integralrechnung
eigene Kapitel bekommen haben), zur Linearen Algebra mit
analytischer Geometrie sowie zur Stochastik werden
schulbuch-übliche Aufgaben vorgerechnet, in nachfolgenden
Übungskapiteln findet man weitere kleinere und
größere Aufgabenstellungen zum Selberrechnen mit
anschließender Lösung (z.T. an alte bayrische
Zentralabitur-Aufgaben angelehnt bzw. daher entnommen).
Beeindruckend ist die Breite des abgedeckten Stoffs, gerade auch
in der andernorts oft immer noch stiefmütterlich behandelten
Stochastik. Störend ist hingegen, dass wirklich nur
gerechnet wird und Erklärungen weitestgehend fehlen: so
steht z.B. nirgends, warum man etwa bei der Kurvendiskussion
f ' (x)=0 setzt, um Kandidaten für Extrem- oder
Sattelstellen zu finden. Auch weitere Kriterien werden zwar
gelegentlich benutzt, aber nie erläutert (der Abschnitt 2.5
'Grundlagen zur Kurvendiskussion' hat daher den Namen nicht
verdient, auch wenn es dort einige Definitionsmengen-,
Symmetrie-, Tangenten- und Nullstellenbestimmungen sowie
Beispiel-Diskussionen für je eine ganzrationale,
gebrochenrationale und trigonometrische Funktion gibt -- aber
eben keine Grundlagen). Ähnliches gilt auch für alle
anderen Kapitel und Themen. Insofern eignet sich das Buch
wirklich nur für Schülerinnen und Schüler, die
für Erklärungen und zum Verständnis auf andere
Quellen zugreifen können und hier nur das rezepthafte
Durchrechnen sehen und üben wollen (auch die
Aufgabensammlung auf DVD liefert als Kontroll-Lösungen immer
nur eine Folge unkommentierter Rechenschritte) -- oder für
Lehrerinnen und Lehrer als Materialvorrat für weitere
(Haus-)Aufgaben zusätzlich zum Schulbuch. Zur Vorbereitung
auf mündliche Prüfungen oder um den Sinn der Verfahren
einzusehen, eignet sich dieses Buch nicht! Der Untertitel des
Buchs "Der komplette Abiturstoff leicht verständlich" ist
insofern irreführend. Georg Glaeser: Der
mathematische Werkzeugkasten - Anwendungen in Natur und
Technik. Jokers edition 2007 (378 Seiten) für 12,95
€. [Die hier besprochenen Ausgabe, basierend auf der
Auflage von 2004, gibt's allenfalls noch gebraucht. Seit
September 2021 ist die wesentlich erweiterte, jetzt 583 Seiten
umfassende 5. Auflage zum Preis von 34,99€ aktuell]
Georg Glaeser: Der
mathematische Werkzeugkasten - Anwendungen in Natur und
Technik. Jokers edition 2007 (378 Seiten) für 12,95
€. [Die hier besprochenen Ausgabe, basierend auf der
Auflage von 2004, gibt's allenfalls noch gebraucht. Seit
September 2021 ist die wesentlich erweiterte, jetzt 583 Seiten
umfassende 5. Auflage zum Preis von 34,99€ aktuell]
 Alex Reinhart: Statistics done wrong -
Deutsche Ausgabe: Statistik richtig anwenden und Fehler
vermeiden. 208 Seiten. mitp-Verlag 2016. ISBN
978-3-95845-252-7. Originalpreis 24,99 €
Alex Reinhart: Statistics done wrong -
Deutsche Ausgabe: Statistik richtig anwenden und Fehler
vermeiden. 208 Seiten. mitp-Verlag 2016. ISBN
978-3-95845-252-7. Originalpreis 24,99 €